
已知函数f(x)是(-∞,+∞)上的增函数,a,b∈R.
(1)若a+b≥0,求证:f(a)+f(b)≥f(-a)+f(-b);
(2)判断(1)中命题的逆命题是否成立,并证明你的结论.
(1) 证明:∵a+b≥0,∴a≥-b. 由f(x)的单调性得f(a)≥f(-b) 又a+b≥0⇒b≥-a⇒f(b)≥f(-a) 两式相加即得:f(a)+f(b)≥f(-a)+f(-b) (2) 逆命题成立,假设a+b<0,那么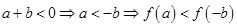 ,
,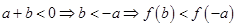 ⇒f(a)+f(b)<f(-a)+f(-b) 这与已知矛盾,故只有a+b≥0
⇒f(a)+f(b)<f(-a)+f(-b) 这与已知矛盾,故只有a+b≥0
解析试题分析:(1)证明:∵a+b≥0,∴a≥-b. 2分
由已知f(x)的单调性得f(a)≥f(-b).
又a+b≥0⇒b≥-a⇒f(b)≥f(-a). 4分
两式相加即得:f(a)+f(b)≥f(-a)+f(-b). 6分
(2)逆命题:
f(a)+f(b)≥f(-a)+f(-b)⇒a+b≥0. 8分
下面用反证法证之.
假设a+b<0,那么: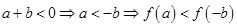
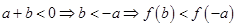
⇒f(a)+f(b)<f(-a)+f(-b). 10分
这与已知矛盾,故只有a+b≥0.逆命题得证. 12分
考点:函数单调性与反证法
点评:单调性的定义:在定义域的某个区间上,若有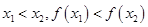 则函数为增函数,若有
则函数为增函数,若有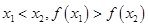 则函数为减函数;反证法证明的大体步骤:假设要证明的结论反面成立,借此推出与已知或定理发生矛盾,推翻假设肯定原结论成立
则函数为减函数;反证法证明的大体步骤:假设要证明的结论反面成立,借此推出与已知或定理发生矛盾,推翻假设肯定原结论成立


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
定义在R上的函数f(x)是最小正周期为2的奇函数, 且当x∈(0, 1)时, f (x)=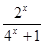 .
.
(1)求f (x)在[-1, 1]上的解析式;
(2)证明f (x)在(—1, 0)上时减函数;
(3)当λ取何值时, 不等式f (x)>λ在R上有解?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知正比例函数y=2x的图像l1与反比例函数y= 的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
(1)求反比例函数的解析式;
(2)求△DOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com