
已知函数
(1)若 在[-3,2]上具有单调性,求实数
在[-3,2]上具有单调性,求实数 的取值范围。
的取值范围。
(2)若 的
的 有最小值为-12,求实数
有最小值为-12,求实数 的值;
的值;
(1)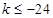 或
或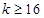 ;(2)
;(2)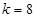 或
或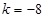
解析试题分析:(1)二次函数的单调性与对称轴有关,单调区间在对称轴的一侧,可数形结合解题;  图像开口上, 对称轴为
图像开口上, 对称轴为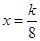 ,区间
,区间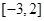 在对称轴左侧
在对称轴左侧 为单调减函数, 区间
为单调减函数, 区间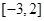 在对称轴右侧
在对称轴右侧 为单调增函数,
为单调增函数,
(2)二次函数在区间上的最值在端点处或顶点处,遇到对称轴或区间含有待定的字母,则要按对称轴在不在区间内以及区间中点进行讨论.  图像开口上,当对称轴为
图像开口上,当对称轴为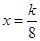 在区间
在区间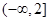 内时,最小值位于对称轴处; 当区间
内时,最小值位于对称轴处; 当区间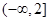 在对称轴左侧
在对称轴左侧 为单调减函数,最小值位于右端点处.
为单调减函数,最小值位于右端点处.
试题解析:
(1)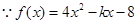 的对称轴为
的对称轴为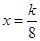
又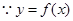 在
在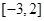 上具有单调性
上具有单调性
所以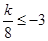 或
或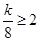
即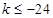 或
或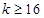
(2) 由 在
在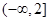 有最小值为
有最小值为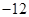
Ⅰ.当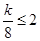 即
即 时
时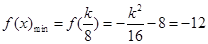
解得: 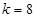 或
或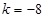
Ⅱ.当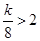 即
即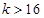 时
时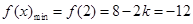
解得: 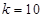 (舍)
(舍)
综上所述: 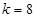 或
或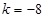
考点:二次函数单调性与最值.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式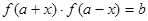 对定义域中的每一个
对定义域中的每一个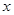 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(Ⅰ)判断函数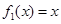 是否为 “(
是否为 “( )型函数”,并说明理由;
)型函数”,并说明理由;
(Ⅱ)若函数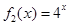 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对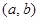 ;,
;,
(Ⅲ)已知函数 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对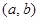 为
为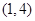 .当
.当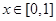 时,
时,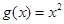
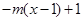
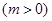 ,若当
,若当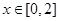 时,都有
时,都有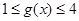 ,试求
,试求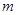 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度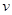 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当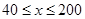 时,车流速度
时,车流速度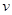 是车流密度
是车流密度 的一次函数.(1)当
的一次函数.(1)当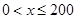 时,求函数
时,求函数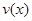 的表达式;
的表达式;
(2)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位: 辆/小时)f
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位: 辆/小时)f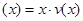 ,
,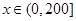 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图是某重点中学学校运动场平面图,运动场总面积15000平方米,运动场是由一个矩形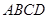 和分别以
和分别以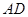 、
、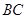 为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,
为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,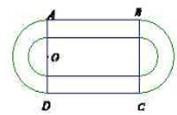
(Ⅰ)设半圆的半径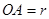 (米),写出塑胶跑道面积
(米),写出塑胶跑道面积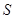 与
与 的函数关系式
的函数关系式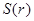 ;
;
(Ⅱ)由于受运动场两侧看台限制, 的范围为
的范围为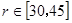 ,问当
,问当 为何值时,运动场造价最低(第2问
为何值时,运动场造价最低(第2问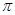 取3近似计算).
取3近似计算).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了降低能损耗,最近上海对新建住宅的屋顶和外墙都要求建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=(0≤x≤10),若不建隔热层,每年能消耗费用为8万元.设f(x)为隔热层建造费用与20年的能消耗费用之和.
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数 ,
, ,其中实数
,其中实数 .
.
(1)若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)当函数 与
与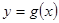 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 的最小值为
的最小值为 ,求
,求 的值域;
的值域;
(3)若 与
与 在区间
在区间 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com