
已知函数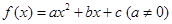 满足
满足 ,对任意
,对任意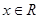 都有
都有 ,且
,且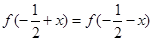 .
.
(1)求函数 的解析式;
的解析式;
(2)是否存在实数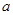 ,使函数
,使函数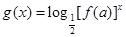 在
在 上为减函数?若存在,求出实数
上为减函数?若存在,求出实数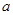 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(1) ;(2)存在实数
;(2)存在实数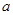 ,
, .
.
解析试题分析:(1)根据 求得
求得 ;
;
根据对任意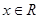 ,有
,有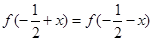 ,确定
,确定 图像的对称轴为直线
图像的对称轴为直线 ,求得
,求得 ;
;
利用对任意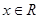 都有
都有 ,转化成
,转化成 对任意
对任意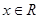 成立,解得
成立,解得 .
.
(2)化简函数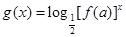
 ,其定义域为
,其定义域为 ,
,
令 ,利用复合函数的单调性,得到
,利用复合函数的单调性,得到 求解,得
求解,得 ,肯定存在性.
,肯定存在性.
试题解析:
(1)由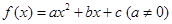 及
及 ∴
∴ 1分
1分
又对任意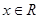 ,有
,有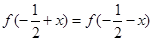
∴ 图像的对称轴为直线
图像的对称轴为直线 ,则
,则 ,∴
,∴ 3分
3分
又对任意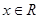 都有
都有 ,
,
即 对任意
对任意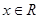 成立,
成立,
∴ ,故
,故 6分
6分
∴ 7分
7分
(2)由(1)知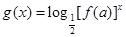
 ,其定义域为
,其定义域为 8分
8分
令
要使函数 在
在 上为减函数,
上为减函数,
只需函数 在
在 上为增函数, 11分
上为增函数, 11分
由指数函数的单调性,有 ,解得
,解得 13分
13分
故存在实数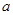 ,当
,当 时,函数
时,函数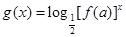 在
在 上为减函数 14分
上为减函数 14分
考点:二次函数的图象和性质,待定系数法,复合函数的单调性,对数函数的性质.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:解答题
已知函数 ,点
,点 、
、 在函数
在函数 的图象上,
的图象上,
点 在函数
在函数 的图象上,设
的图象上,设
 .
.
(1)求数列 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列 的前
的前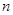 项和为
项和为 ;
;
(3)已知 ,记数列
,记数列 的前
的前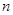 项和为
项和为 ,数列
,数列 的前
的前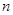 项和为
项和为 ,试比较
,试比较 与
与 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市电力公司在电力供不应求时期,为了居民节约用电,采用“阶梯电价”方法计算电价,每月用电不超过 度时,按每度
度时,按每度 元计费,每月用电超过
元计费,每月用电超过 度时,超过部分按每度
度时,超过部分按每度 元计费,每月用电超过
元计费,每月用电超过 度时,超过部分按每度
度时,超过部分按每度 元计费
元计费
(Ⅰ)设每月用电 度,应交电费
度,应交电费 元,写出
元,写出 关于
关于 的函数;
的函数;
(Ⅱ)已知小王家第一季度缴费情况如下:
| 月份 | 1 | 2 | 3 | 合计 |
| 缴费金额 | 87元 | 62元 | 45元8角 | 194元8角 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)是定义在R上的奇函数,且f(x)的图象关于直线x=1对称.
(1)求证:f(x)是周期为4的周期函数;
(2)若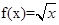 (0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义在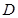 上的函数
上的函数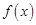 ,如果满足:对任意
,如果满足:对任意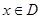 ,存在常数
,存在常数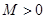 ,使得
,使得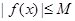 成立,则称
成立,则称 是
是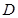 上的有界函数,其中
上的有界函数,其中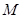 称为函数
称为函数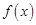 的上界.
的上界.
下面我们来考虑两个函数: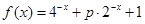 ,
,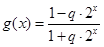 .
.
(Ⅰ)当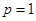 时,求函数
时,求函数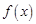 在
在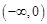 上的值域,并判断函数
上的值域,并判断函数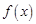 在
在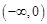 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(Ⅱ)若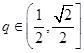 ,函数
,函数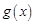 在
在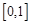 上的上界是
上的上界是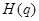 ,求
,求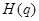 的取值范围;
的取值范围;
(Ⅲ)若函数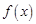 在
在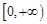 上是以
上是以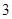 为上界的有界函数, 求实数
为上界的有界函数, 求实数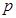 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
停车场预计“十·一”国庆节这天将停放大小汽车1200辆次,该停车场的收费标准为:大车每辆次10元,小车每辆次5元.根据预计,解答下面的问题:
(1)写出国庆节这天停车场的收费金额y(元)与小车停放辆次x(辆)之间的函数关系式,并指出自变量x的取值范围;
(2)如果国庆节这天停放的小车辆次占停车总辆次的65%~85%,请你估计国庆节这天该停车场收费金额的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数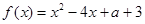 ,
,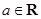 .
.
(Ⅰ)若函数 的图象与
的图象与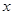 轴无交点,求
轴无交点,求 的取值范围;
的取值范围;
(Ⅱ)若函数 在
在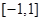 上存在零点,求
上存在零点,求 的取值范围;
的取值范围;
(Ⅲ)设函数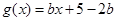 ,
,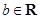 .当
.当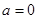 时,若对任意的
时,若对任意的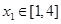 ,总存在
,总存在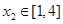 ,使得
,使得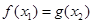 ,求
,求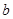 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com