
已知函数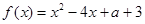 ,
,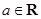 .
.
(Ⅰ)若函数 的图象与
的图象与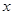 轴无交点,求
轴无交点,求 的取值范围;
的取值范围;
(Ⅱ)若函数 在
在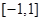 上存在零点,求
上存在零点,求 的取值范围;
的取值范围;
(Ⅲ)设函数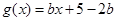 ,
,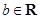 .当
.当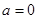 时,若对任意的
时,若对任意的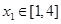 ,总存在
,总存在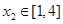 ,使得
,使得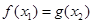 ,求
,求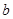 的取值范围.
的取值范围.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)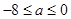 ;(Ⅲ)
;(Ⅲ)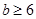 或
或 .
.
解析试题分析:(Ⅰ)函数 的图像与
的图像与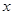 轴无交点,那么函数对应的方程的判别式
轴无交点,那么函数对应的方程的判别式 ,解不等式即可;(Ⅱ)先判断函数
,解不等式即可;(Ⅱ)先判断函数 在闭区间
在闭区间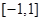 的单调性,然后根据零点存在性定理,可知
的单调性,然后根据零点存在性定理,可知 ,解方程组求得同时满足两个表达式的
,解方程组求得同时满足两个表达式的 的取值范围;(Ⅲ)若对任意的
的取值范围;(Ⅲ)若对任意的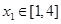 ,总存在
,总存在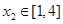 ,使
,使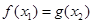 ,只需函数
,只需函数 的值域为函数
的值域为函数 值域的子集即可.先求出函数
值域的子集即可.先求出函数 在区间
在区间 上的值域是
上的值域是 ,然后判断函数
,然后判断函数 的值域.分
的值域.分 ,
, ,
, 三种情况进行分类讨论,当
三种情况进行分类讨论,当 时,函数
时,函数 是一次函数,最值在两个区间端点处取得,所以假设其值域是
是一次函数,最值在两个区间端点处取得,所以假设其值域是 ,那么就有
,那么就有 成立,解相应的不等式组即可.
成立,解相应的不等式组即可.
试题解析:(Ⅰ)若函数 的图象与
的图象与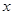 轴无交点,则方程
轴无交点,则方程 的判别式
的判别式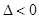 ,
,
即 ,解得
,解得 . 3分
. 3分
(Ⅱ)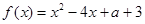 的对称轴是
的对称轴是 ,所以
,所以 在
在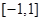 上是减函数,
上是减函数, 在
在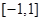 上存在零点,则必有:
上存在零点,则必有: ,即
,即 ,
,
解得: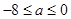 ,故实数
,故实数 的取值范围为
的取值范围为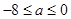 ; 8分
; 8分
(Ⅲ)若对任意的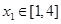 ,总存在
,总存在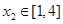 ,使
,使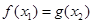 ,只需函数
,只需函数 的值域为函数
的值域为函数 值域的子集.当
值域的子集.当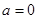 时,
时,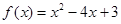 的对称轴是
的对称轴是 ,所以
,所以 的值域为
的值域为 , 下面求
, 下面求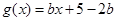 ,
,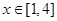 的值域,
的值域,
①当 时,
时, ,不合题意,舍;
,不合题意,舍;
②当 时,
时,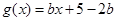 的值域为
的值域为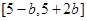 ,只需要:
,只需要: ,解得
,解得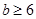 ;
;
③当 时,
时,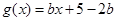 的值域为
的值域为 ,只需要:
,只需要: ,解得
,解得 ;
;
综上:实数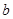 的取值范围
的取值范围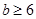 或
或 . 14分
. 14分
考点:1.方程根的个数与判别式的关系;2.零点存在性定理;3.二次函数在闭区间上的值域;4.一次函数的单调性;5.二次函数的图像与性质


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:解答题
相关部门对跳水运动员进行达标定级考核,动作自选,并规定完成动作成绩在八分及以上的定为达标,成绩在九分及以上的定为一级运动员. 已知参加此次考核的共有56名运动员.
(1)考核结束后,从参加考核的运动员中随机抽取了8人,发现这8人中有2人没有达标,有3人为一级运动员,据此请估计此次考核的达标率及被定为一级运动员的人数;
(2)经过考核,决定从其中的A、B、C、D、E五名一级运动员中任选2名参加跳水比赛(这五位运动员每位被选中的可能性相同). 写出所有可能情况,并求运动员E被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数 ,
, ,其中实数
,其中实数 .
.
(1)若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)当函数 与
与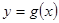 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 的最小值为
的最小值为 ,求
,求 的值域;
的值域;
(3)若 与
与 在区间
在区间 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
近年来,网上购物已经成为人们消费的一种趋势。假设某淘宝店的一种装饰品每月的销售量y(单位:千件)与销售价格x(单位:元/件)满足关系式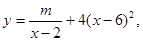 其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数 ,
, ,其中实数
,其中实数 .
.
(1)若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)当函数 与
与 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 的最小值为
的最小值为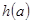 ,求
,求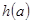 的值域;
的值域;
(3)若 与
与 在区间
在区间 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (
( 为常数,
为常数, 为自然对数的底)
为自然对数的底)
(1)当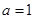 时,求
时,求 的单调区间;
的单调区间;
(2)若函数 在
在 上无零点,求
上无零点,求 的最小值;
的最小值;
(3)若对任意的 ,在
,在 上存在两个不同的
上存在两个不同的 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com