
已知函数 (
( 为常数,
为常数, 为自然对数的底)
为自然对数的底)
(1)当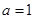 时,求
时,求 的单调区间;
的单调区间;
(2)若函数 在
在 上无零点,求
上无零点,求 的最小值;
的最小值;
(3)若对任意的 ,在
,在 上存在两个不同的
上存在两个不同的 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.
(1) 的减区间为
的减区间为 ,增区间为
,增区间为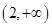 ;
;
(2) 的最小值为
的最小值为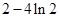 ;
;
(3) 的取值范围是
的取值范围是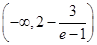 .
.
解析试题分析:(1)将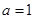 代入函数
代入函数 的解析式,利用导数求出
的解析式,利用导数求出 的单调递增区间和递减区间;(2)将函数
的单调递增区间和递减区间;(2)将函数 在
在 上无零点的问题转化为直线
上无零点的问题转化为直线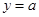 与曲线
与曲线 在区间
在区间 上无交点,利用导数确定函数
上无交点,利用导数确定函数 在区间
在区间 上的图象,进而求出参数
上的图象,进而求出参数 的取值范围,从而确定
的取值范围,从而确定 的最小值;(3)先研究函数
的最小值;(3)先研究函数 在
在 上的单调性,然后再将题干中的条件进行适当转化,利用两个函数的最值或端点值进行分析,列出相应的不等式,从而求出
上的单调性,然后再将题干中的条件进行适当转化,利用两个函数的最值或端点值进行分析,列出相应的不等式,从而求出 的取值范围.
的取值范围.
试题解析:(1)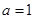 时,
时,
由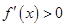 得
得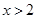
 得
得
故 的减区间为
的减区间为 增区间为
增区间为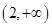 3分
3分
(2)因为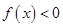 在
在 上恒成立不可能
上恒成立不可能
故要使 在
在 上无零点,只要对任意的
上无零点,只要对任意的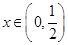 ,
,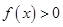 恒成立
恒成立
即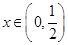 时,
时, 5分
5分
令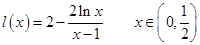
则
再令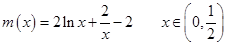
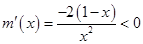 于是在
于是在 上
上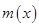 为减函数
为减函数
故
 在
在 上恒成立
上恒成立 在
在 上为增函数
上为增函数 在
在 上恒成立
上恒成立
又
故要使 恒成立,只要
恒成立,只要
若函数 在
在 上无零点,
上无零点, 的最小值为
的最小值为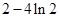 8分
8分
(3)
当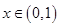 时,
时, ,
,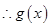 为增函数
为增函数
当 时,
时,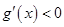 ,
,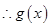 为减函数
为减函数
 函数
函数 在
在 上的值域为
上的值域为 9分
9分
当 时,不合题意
时,不合题意
当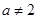 时,
时,
故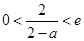
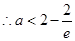 ①
①


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
停车场预计“十·一”国庆节这天将停放大小汽车1200辆次,该停车场的收费标准为:大车每辆次10元,小车每辆次5元.根据预计,解答下面的问题:
(1)写出国庆节这天停车场的收费金额y(元)与小车停放辆次x(辆)之间的函数关系式,并指出自变量x的取值范围;
(2)如果国庆节这天停放的小车辆次占停车总辆次的65%~85%,请你估计国庆节这天该停车场收费金额的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数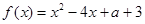 ,
,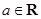 .
.
(Ⅰ)若函数 的图象与
的图象与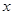 轴无交点,求
轴无交点,求 的取值范围;
的取值范围;
(Ⅱ)若函数 在
在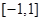 上存在零点,求
上存在零点,求 的取值范围;
的取值范围;
(Ⅲ)设函数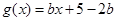 ,
,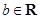 .当
.当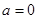 时,若对任意的
时,若对任意的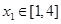 ,总存在
,总存在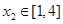 ,使得
,使得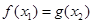 ,求
,求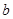 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某投资公司投资甲、乙两个项目所获得的利润分别是P(亿元)和Q亿元),它们与投资额t(亿元)的关系有经验公式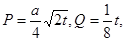 其中
其中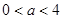 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
(1)求y关于x的解析式,
(2)怎样投资才能使总利润最大,最大值为多少?.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数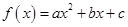 .
.
(1)若对任意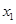 、
、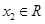 ,且
,且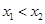 ,都有
,都有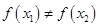 ,求证:关于
,求证:关于 的方程
的方程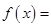
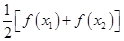 有两个不相等的实数根且必有一个根属于
有两个不相等的实数根且必有一个根属于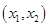 ;
;
(2)若关于 的方程
的方程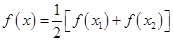 在
在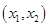 上的根为
上的根为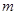 ,且
,且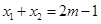 ,设函数
,设函数 的图象的对称轴方程为
的图象的对称轴方程为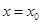 ,求证:
,求证: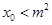 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 .
.
⑴ 求函数 的单调区间;
的单调区间;
⑵ 如果对于任意的 ,
, 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;
⑶ 设函数 ,
, . 过点
. 过点 作函数
作函数 图像的所有切线,令各切点的横坐标构成数列
图像的所有切线,令各切点的横坐标构成数列 ,求数列
,求数列 的所有项之和
的所有项之和 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com