停车场预计“十·一”国庆节这天将停放大小汽车1200辆次，该停车场的收费标准为：大车每辆次10元，小车每辆次5元．根据预计，解答下面的问题：
(1)写出国庆节这天停车场的收费金额y(元)与小车停放辆次x(辆)之间的函数关系式，并指出自变量x的取值范围；
(2)如果国庆节这天停放的小车辆次占停车总辆次的65%～85%，请你估计国庆节这天该停车场收费金额的范围．
科目：高中数学 来源： 题型：解答题
记数列{
}的前n项和为为
，且＋＋n＝0（n∈N*）恒成立．
（1）求证：数列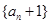
是等比数列；
（2）已知2是函数f（x）＝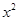
＋ax－1的零点，若关于x的不等式f（x）≥对任意n∈N﹡在x∈（－∞，λ]上恒成立，求实常数λ的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
为了降低能损耗，最近上海对新建住宅的屋顶和外墙都要求建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能消耗费用C(单位：万元)与隔热层厚度x(单位：cm)满足关系：C(x)＝(0≤x≤10)，若不建隔热层，每年能消耗费用为8万元．设f(x)为隔热层建造费用与20年的能消耗费用之和．
(1)求k的值及f(x)的表达式；
(2)隔热层修建多厚时，总费用f(x)达到最小，并求最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某连锁分店销售某种商品,每件商品的成本为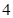
元,并且每件商品需向总店交
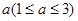元的管理费,预计当每件商品的售价为
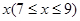元时,一年的销售量为
万件．
（Ⅰ）求该连锁分店一年的利润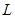
（万元）与每件商品的售价
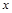的函数关系式
;
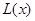（Ⅱ）当每件商品的售价为多少元时,该连锁分店一年的利润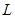最大,并求出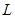的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
相关部门对跳水运动员进行达标定级考核，动作自选，并规定完成动作成绩在八分及以上的定为达标，成绩在九分及以上的定为一级运动员. 已知参加此次考核的共有56名运动员.
（1）考核结束后，从参加考核的运动员中随机抽取了8人，发现这8人中有2人没有达标，有3人为一级运动员，据此请估计此次考核的达标率及被定为一级运动员的人数；
（2）经过考核，决定从其中的A、B、C、D、E五名一级运动员中任选2名参加跳水比赛（这五位运动员每位被选中的可能性相同）. 写出所有可能情况，并求运动员E被选中的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
（
为常数，
为自然对数的底）
（1）当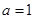
时，求
的单调区间；
（2）若函数在
上无零点，求的最小值；
（3）若对任意的
，在
上存在两个不同的
使得
成立，求的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；（2）
．
辆时，大车停放辆次为
辆，因为大车每辆次10元，小车每辆次5元，则可得
与
8分
在
上为减函数， 10分
12分
的定义域为
，且同时满足以下三个条件：①
；②对任意的
，都有
；③当
时总有
．
的值；
时，恒有
．
满足
，对任意
都有
，且
．
的解析式；
，使函数
在
上为减函数？若存在，求出实数
在区间
上有最大值4，最小值1，
的值。
不等式
在区间
上恒成立，求实数k的取值范围？