
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值(精确到1辆/小时).
(1)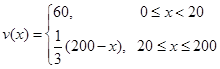 ;(2)当车流密度为100辆/千米时 ,车流量可以达到最大,最大值约为3333辆/小时.
;(2)当车流密度为100辆/千米时 ,车流量可以达到最大,最大值约为3333辆/小时.
解析试题分析:(1)当0≤x≤20时,速度v(x)是一个常数60;当0≤x≤20时,设v(x)=ax+b.
当x =20时,v=60;当x=200时,v=0,代入v(x)=ax+b得:20a+b=60,200a+b=0.
解这个方程组便可得a、b的值,从而得函数v(x)的表达式.
(2)由(1)可得f(x)=x·v(x)的解析式,该函数是一个分段函数,所以分别求出每一段的最大值,然后比较它们的大小,取大者即车流量的最大值.
试题解析:(1)由题意:当0≤x≤20时,v(x)=60;当20≤x≤200时,设v(x)=ax+b,
再由已知条件得200a+b=0,20a+b=60,解得a=-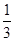 ,b=
,b=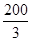 .
.
故函数v(x)的表达式为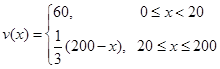
(2)依题意并由(1)可得: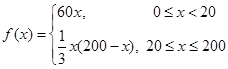 .
.
当0≤x≤20时,f(x)为增函数,故当x=20时,其最大值为60×20=1200;
当20≤x≤200时,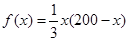 ≤
≤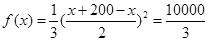 ,
,
当且仅当x=200-x,即x=100时,等号成立.
所以,当x=100时,f(x)在区间[20,200]上取得最大值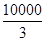 .
.
综上,当x=100时,f(x)在区间[0,200]上取得最大值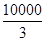 ≈3333,
≈3333,
即当车流密度为100辆/千米时 ,车流量可以达到最大,最大值约为3333辆/小时.
考点:1、函数的应用;2、分段函数;3、函数的最值;4、重要不等式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
相关部门对跳水运动员进行达标定级考核,动作自选,并规定完成动作成绩在八分及以上的定为达标,成绩在九分及以上的定为一级运动员. 已知参加此次考核的共有56名运动员.
(1)考核结束后,从参加考核的运动员中随机抽取了8人,发现这8人中有2人没有达标,有3人为一级运动员,据此请估计此次考核的达标率及被定为一级运动员的人数;
(2)经过考核,决定从其中的A、B、C、D、E五名一级运动员中任选2名参加跳水比赛(这五位运动员每位被选中的可能性相同). 写出所有可能情况,并求运动员E被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数 ,
, ,其中实数
,其中实数 .
.
(1)若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)当函数 与
与 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 的最小值为
的最小值为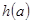 ,求
,求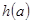 的值域;
的值域;
(3)若 与
与 在区间
在区间 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (
( 为常数,
为常数, 为自然对数的底)
为自然对数的底)
(1)当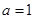 时,求
时,求 的单调区间;
的单调区间;
(2)若函数 在
在 上无零点,求
上无零点,求 的最小值;
的最小值;
(3)若对任意的 ,在
,在 上存在两个不同的
上存在两个不同的 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会超过600件.
(1)设一次订购x件,服装的实际出厂单价为p元,写出函数 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,其中
,其中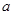 为大于零的常数,
为大于零的常数,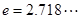 ,函数
,函数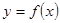 的图像与坐标轴交点处的切线为
的图像与坐标轴交点处的切线为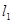 ,函数
,函数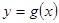 的图像与直线
的图像与直线 交点处的切线为
交点处的切线为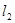 ,且
,且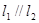 .
.
(I)若在闭区间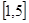 上存在
上存在 使不等式
使不等式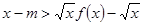 成立,求实数
成立,求实数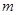 的取值范围;
的取值范围;
(II)对于函数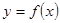 和
和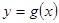 公共定义域内的任意实数
公共定义域内的任意实数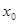 ,我们把
,我们把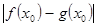 的值称为两函数在
的值称为两函数在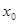 处的偏差.求证:函数
处的偏差.求证:函数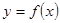 和
和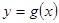 在其公共定义域内的所有偏差都大于2.
在其公共定义域内的所有偏差都大于2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com