解:(1)函数f(x)=x
2-ax-aln(x-1)(a∈R)的定义域是(1,+∞)
当a=1时,
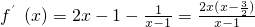
,所以f(x)在

为减函数
在
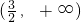
为增函数,所以函数f(x)的最小值为
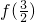
=
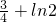
.
(2)
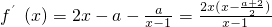
,
若a≤0时,则
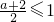
,f(x)=
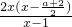
>0在(1,+∞)恒成立,所以f(x)的增区间为(1,+∞).
若a>0,则
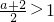
,故当
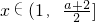
,f′(x)=
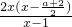
≤0,
当
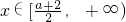
时,f(x)=
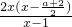
≥0,
所以a>0时f(x)的减区间为
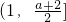
,f(x)的增区间为
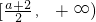
(3)a≥1时,由(2)知f(x)在(1,+∞)的最小值为
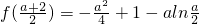
,
令
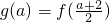
=
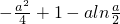
在[1,+∞)上单调递减,
所以
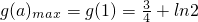
,则
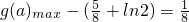
>0,
因此存在实数a(a≥1)使f(x)的最小值大于
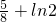
,
故存在实数a(a≥1)使y=f(x)的图象与
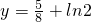
无公共点
分析:(1)先求出函数的定义域,再把a=1代入求出其导函数以及单调区间,即可求出函数f(x)的最值;
(2)先求出函数的导函数,再利用分类讨论思想讨论导函数对应方程根的大小,进而求出函数f(x)的单调区间;
(3)先由(2)得f(x)在(1,+∞)的最小值为
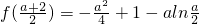
,再求出
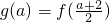
在[1,+∞)上的最大值,让其与
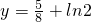
的值相比较即可求得结论.
点评:本题考查了利用导数求闭区间上函数的最值,利用导数研究函数的单调性和最值的应用.求函数在闭区间[a,b]上的最大值与最小值是通过比较函数在(a,b)内所有极值与端点函数f(a),f(b) 比较而得到的.

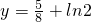 无公共点.
无公共点.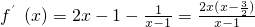 ,所以f(x)在
,所以f(x)在 为减函数
为减函数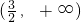 为增函数,所以函数f(x)的最小值为
为增函数,所以函数f(x)的最小值为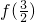 =
=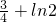 .
.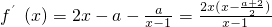 ,
,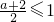 ,f(x)=
,f(x)=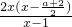 >0在(1,+∞)恒成立,所以f(x)的增区间为(1,+∞).
>0在(1,+∞)恒成立,所以f(x)的增区间为(1,+∞).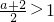 ,故当
,故当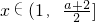 ,f′(x)=
,f′(x)=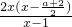 ≤0,
≤0,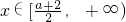 时,f(x)=
时,f(x)=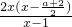 ≥0,
≥0,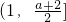 ,f(x)的增区间为
,f(x)的增区间为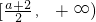
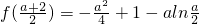 ,
,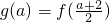 =
=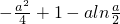 在[1,+∞)上单调递减,
在[1,+∞)上单调递减,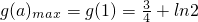 ,则
,则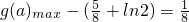 >0,
>0,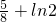 ,
,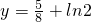 无公共点
无公共点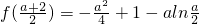 ,再求出
,再求出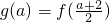 在[1,+∞)上的最大值,让其与
在[1,+∞)上的最大值,让其与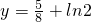 的值相比较即可求得结论.
的值相比较即可求得结论.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<