
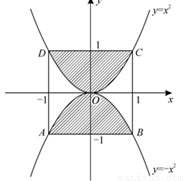
正方形的四个顶点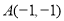 ,
,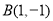 ,
,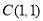 ,
,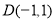 分别在抛物线
分别在抛物线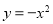 和
和 上,
上,
如图所示.若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是 .
科目:高中数学 来源:2015届湖北省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
已知圆 的方程为
的方程为 ,定直线
,定直线 的方程为
的方程为 .动圆
.动圆 与圆
与圆 外切,且与直线
外切,且与直线 相切.
相切.
(1)求动圆圆心 的轨迹
的轨迹 的方程;
的方程;
(2)直线 与轨迹
与轨迹 相切于第一象限的点
相切于第一象限的点 , 过点
, 过点 作直线
作直线 的垂线恰好经过点
的垂线恰好经过点 ,并交轨迹
,并交轨迹 于异于点
于异于点 的点
的点 ,求直线
,求直线 的方程及
的方程及 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2015届湖北省襄阳市四校高二下学期期中联考文科数学试卷(解析版) 题型:解答题
已知抛物线 ,直线
,直线 ,
, 是抛物线的焦点。
是抛物线的焦点。

(1)在抛物线上求一点 ,使点
,使点 到直线
到直线 的距离最小;
的距离最小;
(2)如图,过点 作直线交抛物线于A、B两点.
作直线交抛物线于A、B两点.
①若直线AB的倾斜角为 ,求弦AB的长度;
,求弦AB的长度;
②若直线AO、BO分别交直线 于
于 两点,求
两点,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2015届湖北省武汉市高三9月调考理科数学试卷(解析版) 题型:解答题
如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH.
(1)求证:AB∥GH;
(2)求平面PAB与平面PCD所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源:2015届湖北省武汉市高三9月调考理科数学试卷(解析版) 题型:选择题
如图,互不相同的点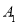 ,
, , ,
, , , 和
, 和 ,
, , ,
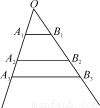
, , , 分别在角O的两条边上,所有
, 分别在角O的两条边上,所有 相互平行,且所有梯形
相互平行,且所有梯形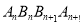 的面积均相等.设
的面积均相等.设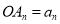 ,若
,若 ,
, ,则
,则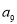 =( )
=( )
A. B.
B.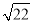 C.
C.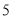 D.
D.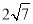
查看答案和解析>>
科目:高中数学 来源:2015届湖北省武汉市高三9月调考文科数学试卷(解析版) 题型:选择题
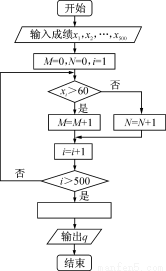
右图是计算某年级500名学生期末考试(满分为100分)及格率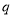 的程序框图,则图中空白框内应填入( )
的程序框图,则图中空白框内应填入( )
A.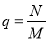 B.
B.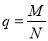 C.
C.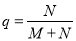 D.
D.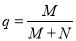
查看答案和解析>>
科目:高中数学 来源:2015届湖北省咸宁市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
不等式 的解集是( )
的解集是( )
A.(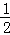 ,+
,+ )
)
B.(3,+ )
)
C.(﹣ ,﹣3)∪(4,+
,﹣3)∪(4,+ )
)
D.(﹣ ,﹣3)∪(
,﹣3)∪(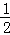 ,+
,+ )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com