
已知函数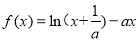 ,其中
,其中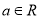 且
且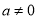 .
.
(1)讨论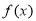 的单调性;
的单调性;
(2) 若不等式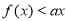 恒成立,求实数
恒成立,求实数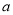 取值范围;
取值范围;
(3)若方程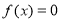 存在两个异号实根
存在两个异号实根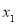 ,
,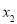 ,求证:
,求证: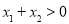
(1)详见解析;(2)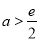 ;(3)证明详见解析.
;(3)证明详见解析.
【解析】
试题分析:本题主要考查导数的运算、利用导数判断导数的单调性、利用导数求函数的单调性、利用导数求函数的最值等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,先求函数的定义域,对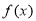 求导,由于
求导,由于 ,所以讨论a的正负,利用
,所以讨论a的正负,利用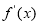 的正负,判断函数的单调性;第二问,结合第一问的结论,当
的正负,判断函数的单调性;第二问,结合第一问的结论,当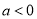 时举一反例证明
时举一反例证明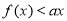 不恒成立,当
不恒成立,当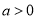 时,将
时,将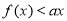 恒成立转化为
恒成立转化为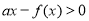 恒成立,令
恒成立,令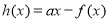 ,利用导数求
,利用导数求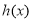 的最小值;第三问,要证
的最小值;第三问,要证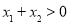 ,需证
,需证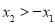 ,令
,令 ,利用函数的单调性,解出
,利用函数的单调性,解出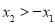 的大小.
的大小.
(1)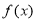 的定义域为
的定义域为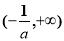 .
.
其导数 2分
2分
①当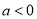 时,
时,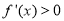 ,函数在
,函数在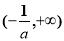 上是增函数;
上是增函数;
②当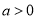 时,在区间
时,在区间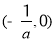 上,
上,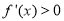 ;在区间(0,+∞)上,
;在区间(0,+∞)上,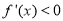 .
.
所以,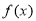 在
在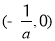 是增函数,在(0,+∞)是减函数. 4分
是增函数,在(0,+∞)是减函数. 4分
(2)当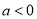 时, 则
时, 则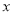 取适当的数能使
取适当的数能使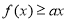 ,比如取
,比如取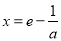 ,
,
能使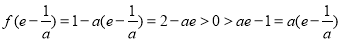 , 所以
, 所以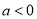 不合题意 6分
不合题意 6分
当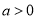 时,令
时,令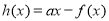 ,则
,则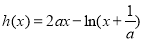
问题化为求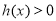 恒成立时
恒成立时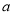 的取值范围.
的取值范围.
由于
 在区间
在区间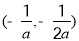 上,
上,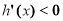 ;在区间
;在区间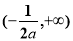 上,
上,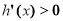 . 8分
. 8分
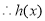 的最小值为
的最小值为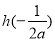 ,所以只需
,所以只需
即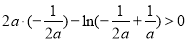 ,
,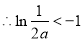 ,
,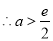 10分
10分
(3)由于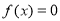 存在两个异号根
存在两个异号根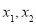 ,不仿设
,不仿设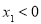 ,因为
,因为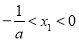 ,所以
,所以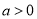 11分
11分
构造函数: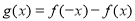 (
(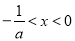 )
)
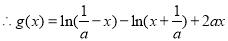
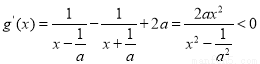
所以函数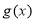 在区间
在区间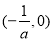 上为减函数.
上为减函数. 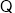
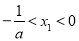 ,则
,则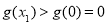 ,
,
于是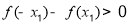 ,又
,又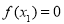 ,
,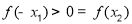 ,由
,由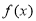 在
在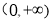 上为减函数可知
上为减函数可知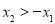 .即
.即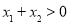 14分
14分
考点:导数的运算、利用导数判断导数的单调性、利用导数求函数的单调性、利用导数求函数的最值.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源:2013-2014学年江苏省南通市高三年级第三次模拟考试文科数学试卷(解析版) 题型:填空题
袋中有2个红球,2个蓝球,1个白球,从中一次取出2个球,则取出的球颜色相同的概率为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:填空题
在Rt△ABC中,CA=CB=2,M,N是斜边AB上的两个动点,且MN=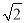 ,则
,则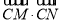 的取值范围为 .
的取值范围为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省韶关市高三4月高考模拟(二模)文科数学试卷(解析版) 题型:填空题
一只艘船以均匀的速度由A点向正北方向航行,如图,开始航行时,从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B点观测灯塔C的方位角为75°,则A到C的距离是__________海里.
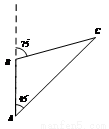
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省肇庆市高三3月第一次模拟文科数学试卷(解析版) 题型:填空题
以平面直角坐标系的原点为极点,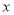 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线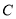 的参数方程为
的参数方程为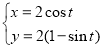 (其中
(其中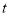 为参数,且
为参数,且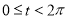 ),则曲线
),则曲线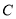 的极坐标方程为 .
的极坐标方程为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com