Question

（本题12分）如图所示，已知圆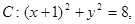定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足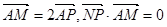，点N的轨迹为曲线E。      

（1）求曲线E的方程； 

（2）若过定点F（0，2）的直线交曲线E于G、H不同的两点，求此直线斜率的取值范围；

（3）若点G在点F、H之间，且满足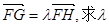的取值范围。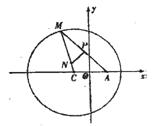

 

Answer 1

【答案】

 

（1）

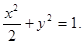
（2）

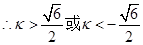
（3）

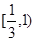
【解析】解：（1）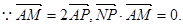

∴NP为AM的垂直平分线，∴|NA|=|NM|……………………1分

又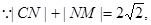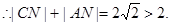……………………2分

∴动点N的轨迹是以点C（－1，0），A（1，0）为焦点的椭圆……………………3分

且椭圆长轴长为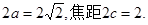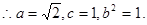……………………5分

∴曲线E的方程为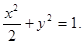……………………(6分)

（2）当直线GH斜率存在时，

设直线GH方程为

得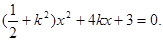……………………7分

由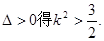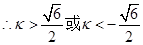……………………8分

（3）设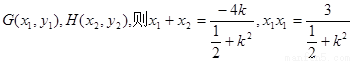

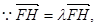
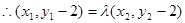
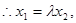
又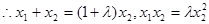[来源:ZXXK.COM]

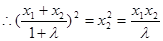
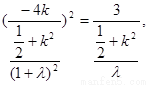    [来源:ZXXK.COM]

整理得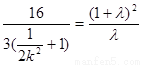                     ……………………10分

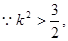
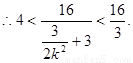
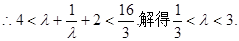
又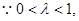

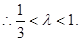……………………(12分)

又当直线GH斜率不存在，方程为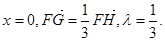

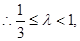即所求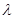的取值范围是 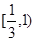       ……………………12分