设函数f(x)=|x-a|-ax,其中0<a<1为常数
(1)解不等式f(x)<0;
(2)试推断函数f(x)是否存在最小值?若存在,求出其最小值;若不存在,说明理由.
解:(1)不等式即为|x-a|<ax,0<a<1,若x≤0,则ax≤0,故不等式不成立;
若x>0,不等式化为(x-a)
2<a
2x
2,即[(1+a)x-a][(1-a)x-a]<0,
由0<a<1可得,
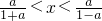
,故不等式解集为{x|
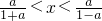
}.
(2)由条件得:f(x)=
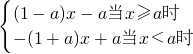
,
∵1>a>0,
∴-(1+a)<0,1-a>0,故函数f(x)在(-∞,a)上是减函数,且在[a,+∞)上是增函数.
故当 x=a 时,f(x)存在最小值f(a).
分析:(1)把f(x)的解析式代入到f(x)<0得到一个不等式,当x小于等于0时得到不等式不成立;当x大于0时,对不等式的两边分别平方,移项后利用平方差公式分解因式,根据a大于0小于1 求出不等式的解集即可.
(2)函数可变为f(x)=
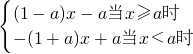
,根据a的范围,运用函数的单调性,得出答案.
点评:此题考查了其他不等式的解法,分类讨论的数学思想,本题还考查函数的最值及其几何意义,解不等式,分类讨论的思想,注意根据函数的形式判断出函数中参数的取值范围,是一道综合题.

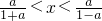 ,故不等式解集为{x|
,故不等式解集为{x|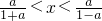 }.
}.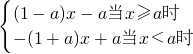 ,
,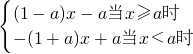 ,根据a的范围,运用函数的单调性,得出答案.
,根据a的范围,运用函数的单调性,得出答案.

 通城学典默写能手系列答案
通城学典默写能手系列答案