
如图,已知四棱锥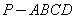 ,底面
,底面 是正方形,PA⊥面
是正方形,PA⊥面 ,点
,点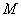 是
是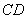 的中点,点
的中点,点 是
是 的中点,连接
的中点,连接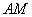 ,
,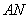
 .
.

(1)求证: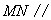 面
面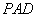 ;
;
(2)若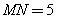 ,
,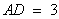 ,求二面角
,求二面角 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
定义在R上的函数f(x)满足f(4)=1, (x)为
(x)为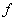 (x)的导函数,函数
(x)的导函数,函数 (x)的图象如图所示。若两正数a,b满足f(2a+b)<1,则
(x)的图象如图所示。若两正数a,b满足f(2a+b)<1,则 的取值范围是( )
的取值范围是( )
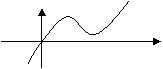

A. 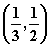 B.
B.  C.
C. 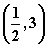 D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数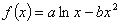 图象上一点P(2,f(2))处的切线方程为
图象上一点P(2,f(2))处的切线方程为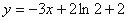 .
.
(Ⅰ)求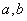 的值;
的值;
(Ⅱ)若方程 在
在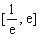 内有两个不等实根,求
内有两个不等实根,求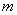 的取值范围(其中
的取值范围(其中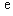 为自然对数的底,
为自然对数的底,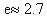 );
);
(Ⅲ)令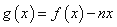 ,如果
,如果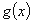 图象与
图象与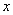 轴交于
轴交于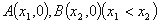 ,AB中点为
,AB中点为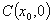 ,求证:
,求证: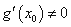 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知an=n×0.8n(n∈N*).
(1) 判断数列{an}的单调性;
(2) 是否存在最小正整数k,使得数列{an}中的任意一项均小于k?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com