
已知an=n×0.8n(n∈N*).
(1) 判断数列{an}的单调性;
(2) 是否存在最小正整数k,使得数列{an}中的任意一项均小于k?请说明理由.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
写出下列数列的一个通项公式:
(1) 1,-3,5,-7,9,…
(2) 1,0,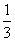 ,0,
,0,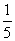 ,0,
,0,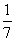 ,…
,…
(3) a,b,a,b,a,b,…
(4) 0.9,0.99,0.999,0.9999,…
(5) 1, …
…
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com