
【题目】如图已知![]() 是边长为
是边长为![]() 的正方形
的正方形![]() 的中心,点
的中心,点![]() 分别是
分别是![]() 的中点,沿对角线
的中点,沿对角线![]() 把正方形
把正方形![]() 折成二面角
折成二面角![]() .
.
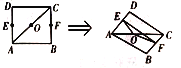
(1)证明:四面体![]() 的外接球的体积为定值,并求出定值;
的外接球的体积为定值,并求出定值;
(2)若二面角![]() 为直二面角,求二面角
为直二面角,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由题意可知,四面体![]() 的外接球始终是以
的外接球始终是以![]() 为直径,即其半径为2,点
为直径,即其半径为2,点![]() 为球心的球,而与二面角
为球心的球,而与二面角![]() 大小无关,再由球的体积公式进行计算,从而问题可得解;(2)由题意可考虑采用坐标法,分别以
大小无关,再由球的体积公式进行计算,从而问题可得解;(2)由题意可考虑采用坐标法,分别以![]() 为
为![]() 轴,建立空间直角坐标系,分别求出二面角两个平面的法向量,再由向量的数量积公式进行运算,从而问题可得解.
轴,建立空间直角坐标系,分别求出二面角两个平面的法向量,再由向量的数量积公式进行运算,从而问题可得解.
试题解析:(1)∵![]() 为定值,与二面角
为定值,与二面角![]() 大小无关,
大小无关,
∴ 四面体![]() 的外接球是以
的外接球是以![]() 为球心,2为半径的球,所以外接球的体积为
为球心,2为半径的球,所以外接球的体积为![]()
(2)以![]() 点为原点,以
点为原点,以![]() 的方向为
的方向为![]() 轴的正方向,建立如图所示的坐标系,
轴的正方向,建立如图所示的坐标系,
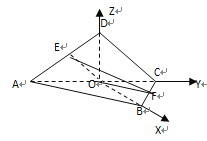
则![]() ,∴
,∴![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则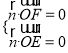 ,即
,即![]() ,令
,令![]() ,则
,则![]() ,
,
∴![]() ,
,
又平面![]() 的法向量 为
的法向量 为![]() ,∴
,∴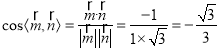 ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,则下面结论正确的是 ( )
,则下面结论正确的是 ( )
A. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍, 纵坐标不变,再把得到的曲线向左平移
倍, 纵坐标不变,再把得到的曲线向左平移![]() 个单位长度, 得到曲线
个单位长度, 得到曲线![]()
B. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍 ,纵坐标不变,再把得到的曲线向左平移
倍 ,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把![]() 上各点的横坐标伸长到原来的
上各点的横坐标伸长到原来的![]() 倍 ,纵坐标不变,再把得到的曲线向左平移
倍 ,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D. 把![]() 上各点的横坐标伸长到原来的
上各点的横坐标伸长到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】陕西省洛川地处北纬35°-36°,东经109°,昼夜温差![]() ,是国内外专家公认的世界最佳苹果优生区,是国家生态建设示范试点.近几年,果农为了提高经济效益,增加了广告和包装的投资费用,5年内果农投入的广告和包装费用
,是国内外专家公认的世界最佳苹果优生区,是国家生态建设示范试点.近几年,果农为了提高经济效益,增加了广告和包装的投资费用,5年内果农投入的广告和包装费用![]() (万元)与销售额
(万元)与销售额![]() (万元)之间有下面对应数据:
(万元)之间有下面对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)假设![]() 与
与![]() 之间线性相关,求回归直线方程;
之间线性相关,求回归直线方程;
(2)预测广告和包装费用为10(万元)时销售额是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的顶点
的顶点![]() 边上的中线
边上的中线![]() 所在直线方程为
所在直线方程为![]() ,
,![]() 边上的高所在直线的方程为
边上的高所在直线的方程为![]() .
.
(1)求![]() 的顶点
的顶点![]() 的坐标;
的坐标;
(2)若圆![]() 经过不同三点
经过不同三点![]() ,且斜率为
,且斜率为![]() 的直线与圆
的直线与圆![]() 相切与点
相切与点![]() ,求圆的方程
,求圆的方程![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知点![]() ,圆
,圆![]()
(I)在极坐标系中,以极点为原点,极轴为![]() 轴正半轴建立平面直角坐标系,取相同的长度单位,求圆
轴正半轴建立平面直角坐标系,取相同的长度单位,求圆![]() 的直角坐标方程;
的直角坐标方程;
(II)求点![]() 到圆
到圆![]() 圆心的距离.
圆心的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com