练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在直三棱柱中， 是线段上一点.

    点.

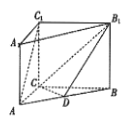
    （1）确定的位置，使得平面平面；

    （2）若平面,设二面角的大小为，求证：

    【答案】（1）见解析（2）

    【解析】试题分析：（1）当时，可证明平面，再根据平面几何知识求解即可；（2）以、、所在直线分别为轴、轴、轴建立如图所示的空间直角坐标系，求出平面的一个法向量及平面的一个法向量，利用空间向量夹角余弦公式可得结果.

    试题解析：（1）当时，∵，∴由射影定理得，∴.

    ∵平面，∴.

    ∵，∴平面.

    又平面，∴当时，平面平面.

    （2）以、、所在直线分别为轴、轴、轴建立如图所示的空间直角坐标系，

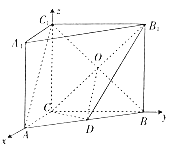
    则， ， .

    连接交于点，则为的中点.

    ∵平面平面，且平面，∴，∴为的中点.

    ∴， ，

    设平面的法向量为，

    则，且，

    令，可取平面的一个法向量，

    而平面的一个法向量为，

    ∴，∵二面角为锐角，

    ∴，又，∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，且.

    （1）若函数在区间上是减函数，求实数的取值范围；

    （2）设函数，当时，恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，我海监船在岛海域例行维权巡航，某时刻航行至处，此时测得其东北方向与它相距32海里的处有一外国船只，且岛位于海监船正东海里处．

    （1）求此时该外国船只与岛的距离；

    （2）观测中发现，此外国船只正以每小时8海里的速度沿正南方向航行，为了将该船拦截在离岛24海里处，不让其进入岛24海里内的海域，试确定海监船的航向，并求其速度的最小值．（参考数据： ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下茎叶图记录了甲，乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊，无法确认，在图中以表示.

    （1）如果，求乙组同学植树棵数的平均数和方差；

    （2）如果，分别从甲，乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率.（注：方差，其中为， ，……， 的平均数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）求函数的单调递增区间；

    （Ⅱ）用反证法证明：在上，不存在不同的两点，，使得的图象在这两点处的切线相互平行．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆.

    （1）若直线过定点，且与圆相切，求的方程；

    （2）若圆的半径为，圆心在直线上，且与圆外切，求圆的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数，若在定义域内存在实数，满足，则称为“局部奇函数”．

    为定义在上的“局部奇函数”；

    曲线与轴交于不同的两点；

    若为假命题， 为真命题，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次水下考古活动中，某一潜水员需潜水米到水底进行考古作业.其用氧量包含一下三个方面：①下潜平均速度为米/分钟，每分钟用氧量为升；②水底作业时间范围是最少分钟最多分钟，每分钟用氧量为升；③返回水面时，平均速度为米/分钟，每分钟用氧量为升.潜水员在此次考古活动中的总用氧量为升.

    （1）如果水底作业时间是分钟，将表示为的函数；

    （2）若，水底作业时间为分钟，求总用氧量的取值范围；

    （3）若潜水员携带氧气升，请问潜水员最多在水下多少分钟（结果取整数）？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图已知是边长为的正方形的中心，点分别是的中点，沿对角线把正方形折成二面角.

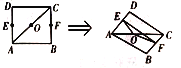
    （1）证明：四面体的外接球的体积为定值，并求出定值；

    （2）若二面角为直二面角，求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案