
设数列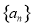 的前
的前 项和为
项和为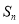 ,且
,且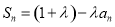 ,其中
,其中 为常数,且
为常数,且
(Ⅰ)证明:数列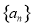 是等比数列;
是等比数列;
(Ⅱ)设数列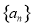 的公比
的公比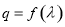 ,数列
,数列 满足
满足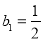 ,
,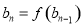 (
(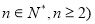 求数列
求数列 的通项公式;
的通项公式;
(Ⅲ)设 ,
, ,数列
,数列 的前
的前 项和为
项和为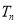
(1)见解析 (2) (3)
(3)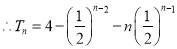
【解析】
试题分析:(1)证明一个数列是否为等差数列的基本方法有两种:一是定义法:证明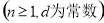 ;二是等差中项法,证明
;二是等差中项法,证明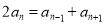 ,若证明一个数列不是等差数列,则只需举出反例即可;(2)根据等差数列的首项和公差求通项公式;根据等比数列的首项和公比求通项公式;注意题中限制条件;(3)一般地,如果数列
,若证明一个数列不是等差数列,则只需举出反例即可;(2)根据等差数列的首项和公差求通项公式;根据等比数列的首项和公比求通项公式;注意题中限制条件;(3)一般地,如果数列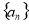 是等差数列,
是等差数列,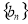 是等比数列,求数列
是等比数列,求数列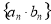 的前
的前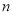 项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列
项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列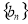 的公比,然后做差求解.
的公比,然后做差求解.
试题解析:(Ⅰ)由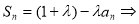
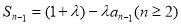 ,
,
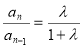
相减得: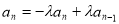 ,∴
,∴
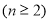 ,
,
∴数列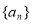 是等比数列.
是等比数列.
(Ⅱ) ,∴
,∴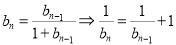 ,
,
∴ 是首项为
是首项为 ,公差为1的等差数列;∴
,公差为1的等差数列;∴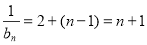 ,
,
∴ .
.
(Ⅲ)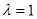 时,
时, ,∴
,∴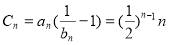 ,
,
∴ , ①
, ①
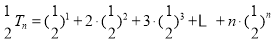 ②
②
① ②得
②得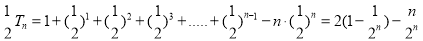 ,
,
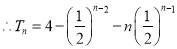 .
.
考点:等比数列的定义及错位相减求数列的和..


科目:高中数学 来源:2015届浙江富阳二中高二下学期第三次质量检测文科数学试卷(解析版) 题型:解答题
已知函数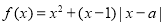 .
.
(1)若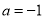 ,解方程
,解方程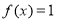 ;
;
(2)若函数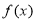 在
在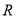 上单调递增,求实数
上单调递增,求实数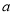 的取值范围;
的取值范围;
(3)若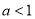 且不等式
且不等式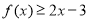 对一切实数
对一切实数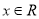 恒成立,求
恒成立,求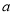 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2015届河南省顶级名校高三入学定位考试理科数学试卷(解析版) 题型:选择题
某学生在一门功课的22次考试中,所得分数如下茎叶图所示,则此学生该门功课考试分数的极差与中位数之和为( )
(A)117 (B)118 (C) 118.5 (D)119.5

查看答案和解析>>
科目:高中数学 来源:2015届河南省顶级名校高三入学定位考试文科数学试卷(解析版) 题型:选择题
如图是一个几何体的三视图,则该几何体的体积是( )
(A)54 (B)27 (C)18 (D) 9
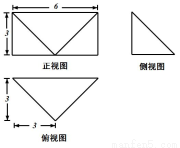
查看答案和解析>>
科目:高中数学 来源:2015届河南省顶级名校高三入学定位考试文科数学试卷(解析版) 题型:选择题
某学生在一门功课的22次考试中,所得分数如下茎叶图所示,则此学生该门功课考试分数的极差与中位数之和为( )
(A)117 (B)118 (C)118.5 (D)119.5

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com