
已知函数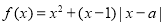 .
.
(1)若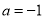 ,解方程
,解方程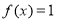 ;
;
(2)若函数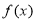 在
在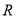 上单调递增,求实数
上单调递增,求实数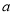 的取值范围;
的取值范围;
(3)若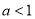 且不等式
且不等式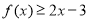 对一切实数
对一切实数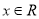 恒成立,求
恒成立,求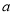 的取值范围
的取值范围
(1) ;(2)
;(2) ;(3)
;(3)
【解析】
试题分析:(1)对于含二次项恒成立的问题,注意讨论二次项系数是否为0,这是学生容易漏掉的地方;恒成立问题一般需转化为最值,利用单调性证明在闭区间的单调性.(2)一元二次不等式在 上恒成立,看开口方向和判别式.(3)含参数的一元二次不等式在某区间内恒成立的问题通常有两种处理方法:一是利用二次函数在区间上的最值来处理;二是分离参数,再去求函数的最值来处理,一般后者比较简单;(4)二次函数、二次方程与二次不等式统称“三个”二次,它们常结合在一起,有关二次函数的问题,数形结合,密切联系图象是探求解题思路的有效方法,一般从:①开口方向;②对称轴位置;③判别式;④端点值符合四个方面分析;二次函数的综合问题应用多涉及单调性与最值或二次方程根的分布问题,解决的主要思路是等价转化,多用到数形结合思想与分类讨论思想.
上恒成立,看开口方向和判别式.(3)含参数的一元二次不等式在某区间内恒成立的问题通常有两种处理方法:一是利用二次函数在区间上的最值来处理;二是分离参数,再去求函数的最值来处理,一般后者比较简单;(4)二次函数、二次方程与二次不等式统称“三个”二次,它们常结合在一起,有关二次函数的问题,数形结合,密切联系图象是探求解题思路的有效方法,一般从:①开口方向;②对称轴位置;③判别式;④端点值符合四个方面分析;二次函数的综合问题应用多涉及单调性与最值或二次方程根的分布问题,解决的主要思路是等价转化,多用到数形结合思想与分类讨论思想.
试题解析:【解析】
(1)当 时,, 故有
时,, 故有
 , 2分
, 2分
当 时,由
时,由 ,有
,有 ,解得
,解得 或
或 3分
3分
当 时,
时, 恒成立 4分
恒成立 4分
∴ 方程的解集为
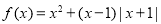 5分
5分
(2) , 7分
, 7分
若 在
在 上单调递增,则有
上单调递增,则有
 , 解得,
, 解得, 9分
9分
∴ 当 时,
时, 在
在 上单调递增 10分
上单调递增 10分
(3)设
则 11分
11分
不等式 对一切实数
对一切实数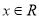 恒成立,等价于不等式
恒成立,等价于不等式 对一切实数
对一切实数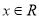 恒成立.
恒成立.

 ,
,
当 时,
时, 单调递减,其值域为
单调递减,其值域为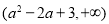 ,
,
由于 ,所以
,所以 成立. 12分
成立. 12分
当 时,由
时,由 ,知
,知 ,
,  在
在 处取最小值,
处取最小值,
令 ,得
,得 ,又
,又 ,所以
,所以
综上, . 14分
. 14分
考点:(1)一元二次不等式的解法;(2)一元二次不等式的单调性;(3)恒成立的问题.


科目:高中数学 来源:2015届浙江省嘉兴市高三新高考调研二文科数学试卷(解析版) 题型:选择题
设m,n是两条不同的直线,α,β,γ是三个不同的平面,
给出下列四个命题:
①m⊥α,n∥α,则m⊥n;
②若α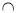 γ=m,β
γ=m,β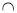 γ=n,m∥n ,则α∥β;
γ=n,m∥n ,则α∥β;
③若α∥β,β∥γ, m⊥α,则m⊥γ;
④若α⊥γ,β⊥γ,则α∥β.
其中正确命题的序号是 ( )
A.①和③ B.②和③ C.③和④ D.①和④
查看答案和解析>>
科目:高中数学 来源:2015届浙江富阳二中高二下学期第三次质量检测理科数学试卷(解析版) 题型:填空题
设等比数列{an}的前n项之和为 ,且2a3+3=S2 , a2+3=S3 , 则该数列的公比
,且2a3+3=S2 , a2+3=S3 , 则该数列的公比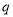 = .
= .
查看答案和解析>>
科目:高中数学 来源:2015届浙江富阳二中高二下学期第三次质量检测理科数学试卷(解析版) 题型:选择题
 的值属于区间( )
的值属于区间( )
A.(-2,-1) B.(1,2) C.(2,3) D.(-3,-2)
查看答案和解析>>
科目:高中数学 来源:2015届浙江富阳二中高二下学期第三次质量检测文科数学试卷(解析版) 题型:填空题
已知点P在直线 上,若在圆
上,若在圆 :
: 上存在两点A,B,使
上存在两点A,B,使 ,则点P的横坐标
,则点P的横坐标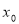 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2015届浙江富阳二中高二下学期第三次质量检测文科数学试卷(解析版) 题型:选择题
在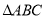 ,三个内角
,三个内角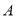 、
、 、
、 所对的边分别为
所对的边分别为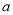 、
、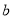 、
、 ,若内角
,若内角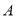 、
、 、
、 依次成等差数列,且不等式
依次成等差数列,且不等式 的解集为
的解集为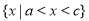 ,则
,则 等于( )
等于( )
A.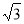 B.4 C.
B.4 C. D.
D.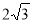
查看答案和解析>>
科目:高中数学 来源:2015届河南省顶级名校高三入学定位考试理科数学试卷(解析版) 题型:填空题
设O是 的三边中垂线的交点,
的三边中垂线的交点, 分别为角
分别为角 对应的边,已知
对应的边,已知 ,则
,则 的范围是___________.
的范围是___________.
查看答案和解析>>
科目:高中数学 来源:2015届河南省东区高二12月月考理科数学试卷(解析版) 题型:解答题
设数列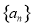 的前
的前 项和为
项和为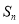 ,且
,且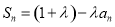 ,其中
,其中 为常数,且
为常数,且
(Ⅰ)证明:数列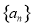 是等比数列;
是等比数列;
(Ⅱ)设数列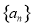 的公比
的公比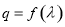 ,数列
,数列 满足
满足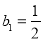 ,
,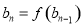 (
(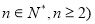 求数列
求数列 的通项公式;
的通项公式;
(Ⅲ)设 ,
, ,数列
,数列 的前
的前 项和为
项和为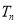
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com