已知函数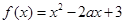
(1)若函数在
的单调递减区间（—∞,2],求函数在区间[3,5]上的最大值.
(2)若函数在在单区间（—∞,2]上是单调递减,求函数
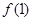的最大值.
科目：高中数学 来源： 题型：解答题
已知函数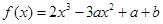
(其中a,b为实常数)。
（Ⅰ）讨论函数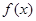
的单调区间：
（Ⅱ）当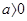
时，函数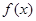有三个不同的零点，证明：
：
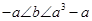（Ⅲ）若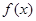在区间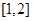
上是减函数，设关于x的方程
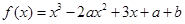的两个非零实数根为
，
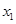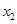。试问是否存在实数m,使得
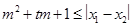对任意满足条件的a及t
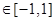恒成立？若存在，求m的取值范围；若不存在，请说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）
某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比．已知投资1万元时两类产品的收益分别为0.125万元和0.5万元（如图）．
（1）分别写出两种产品的收益与投资额的函数关系；
（2）该家庭现有20万元资金，全部用于理财投资，问：怎么分配资金能使投资获得最大收益，其最大收益是多少万元？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(本小题满分10分）宁波市的一家报刊点，从报社买进《宁波日报》的价格是每份0.20元，卖出的价格是每份0.3元，卖不掉的报纸可以以每份0.05元的价格退回报社。在一个月（30天计）里，有20天可以卖出400份，其余10天每天只能卖出250份，但是每天从报社买进的份数必须相同，这个摊主每天从报社买进多少份，才能使得每月所获利润最大？并计算他一个月最多可以赚多少元？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题12分）运货卡车以每小时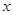
千米的速度匀速行驶130千米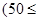
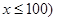（单位：千米/小时）．假设汽油的价格是每升2a元，而汽车每小时耗油
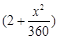升，司机的工资是每小时14a元.（1）求这次行车总费用
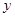关于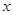的表达式；（2）当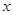为何值时，这次行车的总费用最低，并求出最低费用的值(a为常数) ．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(12分) 若二次函数f(x)=ax2+bx+c(a≠0)的图象关于y轴对称，
且f(-2)＞f(3)，设m＞-n＞0.
(1) 试证明函数f(x)在(0，+∞)上是减函数；
(2) 试比较f(m)和f(n)的大小，并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，且满足
的值；
，
，求
的值。 
，当
时，对应
值的集合为
.
的值；（2）若
，求该函数的最值.
满足条件
，及
.
上的最大和最小值.