
(本小题满分10分)宁波市的一家报刊点,从报社买进《宁波日报》的价格是每份0.20元,卖出的价格是每份0.3元,卖不掉的报纸可以以每份0.05元的价格退回报社。在一个月(30天计)里,有20天可以卖出400份,其余10天每天只能卖出250份,但是每天从报社买进的份数必须相同,这个摊主每天从报社买进多少份,才能使得每月所获利润最大?并计算他一个月最多可以赚多少元?
摊主每天从报买进400份时,每月的利润最大,最大利润为825元。
解析试题分析:若设每天从报社买进x(250≤x≤400,x∈N+)份,则每月共可销售(20x+10×250)份,每份可获利润0.10元,退回报社10(x-250)份,每份亏损0.15元,建立月纯利润函数f(x),再求f(x)的最大值,可得一个月的最大利润.
解:设每天进的报刊数量为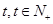 ,获取利润为
,获取利润为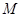 ,则
,则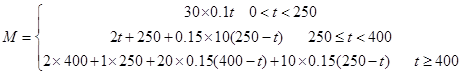 ……………………6分
……………………6分
即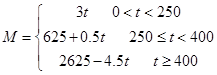 ,当
,当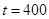 时,
时,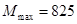 ,摊主每天从报买进400份时,每月的利润最大,最大利润为825元。……………………10分
,摊主每天从报买进400份时,每月的利润最大,最大利润为825元。……………………10分
考点:本试题主要考查了函数模型的构建,考查利用一次函数求解实际问题,把复杂的实际问题转化成数学问题.
点评:利用一次函数的单调性,确定最大利润是解题的关键。体现了运用函数解决问题和分析问题的能力。


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:解答题
(12分)某车间生产一种仪器的固定成本是10000元,每生产一台该仪器需要增加投入100
元,已知总收入满足函数: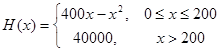 ,其中
,其中 是仪器的月产量.
是仪器的月产量.
(1)将利润表示为月产量的函数(用 表示);
表示);
(2)当月产量为何值时,车间所获利润最大?最大利润是多少元?(总收入=总成本+利润)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数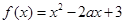
(1)若函数在 的单调递减区间(—∞,2],求函数
的单调递减区间(—∞,2],求函数 在区间[3,5]上的最大值.
在区间[3,5]上的最大值.
(2)若函数在 在单区间(—∞,2]上是单调递减,求函数
在单区间(—∞,2]上是单调递减,求函数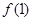 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com