
(本小题12分)运货卡车以每小时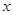 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米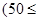
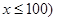 (单位:千米/小时).假设汽油的价格是每升2a元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2a元,而汽车每小时耗油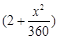 升,司机的工资是每小时14a元.(1)求这次行车总费用
升,司机的工资是每小时14a元.(1)求这次行车总费用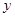 关于
关于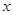 的表达式;(2)当
的表达式;(2)当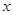 为何值时,这次行车的总费用最低,并求出最低费用的值(a为常数) .
为何值时,这次行车的总费用最低,并求出最低费用的值(a为常数) .
(1)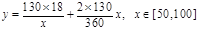 或:
或: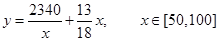
(2)当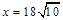 时,这次行车的总费用最低,最低费用为
时,这次行车的总费用最低,最低费用为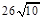 元。
元。
解析试题分析:(1)求出车所用时间,根据汽油的价格是每升2元,而汽车每小时耗油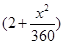 升,司机的工资是每小时14元,可得行车总费用;
升,司机的工资是每小时14元,可得行车总费用;
(2)利用基本不等式,即可求得这次行车的总费用最低.
(1)设行车所用时间为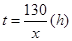 ,
, 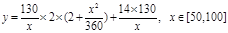
所以,这次行车总费用y关于x的表达式是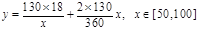 (或:
(或: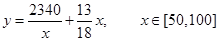 )............6分
)............6分
(2)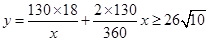 .....................9分
.....................9分
仅当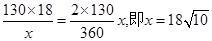 时,上述不等式中等号成立 ...................11分
时,上述不等式中等号成立 ...................11分
答:当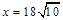 时,这次行车的总费用最低,最低费用为
时,这次行车的总费用最低,最低费用为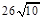 元 ....................12分
元 ....................12分
考点:基本不等式在最值问题中的应用;函数模型的选择与应用.
点评:本题考查函数模型的构建,考查利用基本不等式求最值,确定函数的模型是关键.


科目:高中数学 来源: 题型:解答题
(12分)某车间生产一种仪器的固定成本是10000元,每生产一台该仪器需要增加投入100
元,已知总收入满足函数: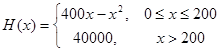 ,其中
,其中 是仪器的月产量.
是仪器的月产量.
(1)将利润表示为月产量的函数(用 表示);
表示);
(2)当月产量为何值时,车间所获利润最大?最大利润是多少元?(总收入=总成本+利润)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数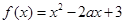
(1)若函数在 的单调递减区间(—∞,2],求函数
的单调递减区间(—∞,2],求函数 在区间[3,5]上的最大值.
在区间[3,5]上的最大值.
(2)若函数在 在单区间(—∞,2]上是单调递减,求函数
在单区间(—∞,2]上是单调递减,求函数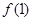 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
(1)分别写出两种产品的收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?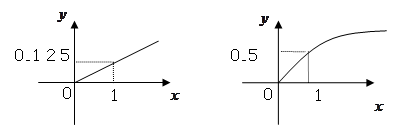
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com