
 如图,棱长为4的正方体ABCD-A1B1C1D1,点A在平面α内,平面ABCD与平面α所成的二面角为30°,则顶点C1到平面α的距离的最大值是( )
如图,棱长为4的正方体ABCD-A1B1C1D1,点A在平面α内,平面ABCD与平面α所成的二面角为30°,则顶点C1到平面α的距离的最大值是( )| A. | 2(2+$\sqrt{2}$) | B. | 2($\sqrt{3}$+$\sqrt{2}$) | C. | 2($\sqrt{3}$+1) | D. | 2($\sqrt{2}$+1) |
分析 如图所示,O在AC上,C1O⊥α,垂足为E,则C1E为所求,∠OAE=30°,由题意,设CO=x,则AO=4$\sqrt{2}$-x,由此可得顶点C1到平面α的距离的最大值.
解答 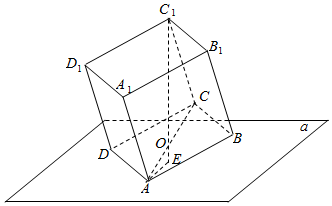 解:如图所示,AC的中点为O,C1O⊥α,
解:如图所示,AC的中点为O,C1O⊥α,
垂足为E,则C1E为所求,∠AOE=30°
由题意,设CO=x,则AO=4$\sqrt{2}$-x,
C1O=$\sqrt{16+{x}^{2}}$,OE=$\frac{1}{2}$OA=2$\sqrt{2}$-$\frac{1}{2}$x,
∴C1E=$\sqrt{16+{x}^{2}}$+2$\sqrt{2}$-$\frac{1}{2}$x,
令y=$\sqrt{16+{x}^{2}}$+2$\sqrt{2}$-$\frac{1}{2}$x,
则y′=$\frac{x}{\sqrt{16+{x}^{2}}}$-$\frac{1}{2}$=0,可得x=$\frac{4}{\sqrt{3}}$,
∴x=$\frac{4}{\sqrt{3}}$,顶点C1到平面α的距离的最大值是2($\sqrt{3}$+$\sqrt{2}$).
故选:B.
点评 本题考查顶点C1到平面α的距离的最大值,考查学生的计算能力,正确作图是关键.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上的一点,BD∥平面AC1E;
如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上的一点,BD∥平面AC1E;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
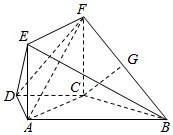 如图,在梯形ABCD中,AB∥CD,AB=2AD=2DC=2CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.
如图,在梯形ABCD中,AB∥CD,AB=2AD=2DC=2CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
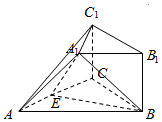 在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.
在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ①③④ | C. | ②④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com