

分析 连接AC,与BD交于O,连接OE,作C1F⊥OE,证明C1O即为所求.
解答 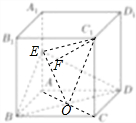 解:如图所示,连接AC,与BD交于O,连接OE,作C1F⊥OE.
解:如图所示,连接AC,与BD交于O,连接OE,作C1F⊥OE.
∵BD⊥平面A1C1CA,BD?平面BDE
∴平面BDE⊥平面A1C1CA,
∵平面BDE∩平面A1C1CA=OE,C1F⊥OE,
∴C1F⊥平面BDE.
△C1OE中,C1E=3,C1O=$\sqrt{6}$,EO=$\sqrt{3}$,
∴C1O2+EO2=C1E2,
∴C1O⊥OE,即O,F重合,
∴点C1到平面BDE的距离为$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题考查点C1到平面BDE的距离的计算,考查学生分析解决问题的能力,属于中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | 15 | D. | 31 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 直三棱柱ABC-A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2,$\overrightarrow{BD}$=λ$\overrightarrow{DC}$.
直三棱柱ABC-A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2,$\overrightarrow{BD}$=λ$\overrightarrow{DC}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
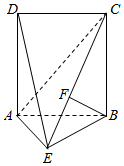 如图,平面ABCD⊥平面ABE,四边形ABCD是边长为2的正方形,且点B在平面ACE上的射影F恰好落在边CE上.
如图,平面ABCD⊥平面ABE,四边形ABCD是边长为2的正方形,且点B在平面ACE上的射影F恰好落在边CE上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
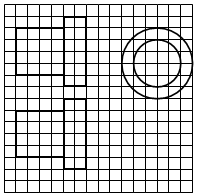 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,现用油漆对该型号零件表面进项防锈处理,若100平方厘米的零件表面约需用油漆10克,那么对100个该型号零件表面进行防锈处理约需油漆( )(π取3.14)
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,现用油漆对该型号零件表面进项防锈处理,若100平方厘米的零件表面约需用油漆10克,那么对100个该型号零件表面进行防锈处理约需油漆( )(π取3.14)| A. | 1.13千克 | B. | 1.45千克 | C. | 1.57千克 | D. | 1.97千克 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,棱长为4的正方体ABCD-A1B1C1D1,点A在平面α内,平面ABCD与平面α所成的二面角为30°,则顶点C1到平面α的距离的最大值是( )
如图,棱长为4的正方体ABCD-A1B1C1D1,点A在平面α内,平面ABCD与平面α所成的二面角为30°,则顶点C1到平面α的距离的最大值是( )| A. | 2(2+$\sqrt{2}$) | B. | 2($\sqrt{3}$+$\sqrt{2}$) | C. | 2($\sqrt{3}$+1) | D. | 2($\sqrt{2}$+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com