
分析 (1)$\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$可知M是AB的中点,根据中点坐标公式求得x1和x2的关系,代入函数解析式即可求得m的值;
(2)由(1)可知,f(x1)+f(x2)=y1+y2=1,采用倒序相加法,即可求求得Sn;
(3)由题意可知当n≥2时,${a_n}=\frac{n-1}{2}$,求得数列{an}的前n项和Tn,由Tn>λ(Sn+1+1),采用分离变量即可求得λ的表达式,即可求得λ的取值范围.
解答 解:(1)∵$\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$,
∴M是AB的中点,设A(x1,y1),B(x2,y2),则
由$\frac{1}{2}({x_1}+{x_2})=\frac{1}{2}$,得x1+x2=1,则x1=1-x2,x2=1-x1,
而$m=\frac{1}{2}({y_1}+{y_2})=\frac{1}{2}[f({x_1})+f({x_2})]$=$\frac{1}{2}(\frac{1}{2}+{log_2}\frac{x_1}{{1-{x_1}}}+\frac{1}{2}+{log_2}\frac{x_2}{{1-{x_2}}})$,
=$\frac{1}{2}(1+{log_2}\frac{x_1}{x_2}+{log_2}\frac{x_2}{x_1})$,
=$\frac{1}{2}(1+{log_2}\frac{x_1}{x_2}•\frac{x_2}{x_1})=\frac{1}{2}$
∴$m=\frac{1}{2}$.
(2)由(1)知:x1+x2=1,f(x1)+f(x2)=y1+y2=1,
${S_n}=f(\frac{1}{n})+f(\frac{2}{n})+…+f(\frac{n-1}{n})$,
${S_n}=f(\frac{n-1}{n})+f(\frac{n-2}{n})+…+f(\frac{1}{n})$,
两式相加,得:$2{S_n}=[f(\frac{1}{n})+f(\frac{n-1}{n})]+[f(\frac{2}{n})+f(\frac{n-2}{n})]+…+[f(\frac{n-1}{n})+f(\frac{1}{n})]$=$\underbrace{1+1+…+1}_{n-1}=n-1$,
∴${S_n}=\frac{n-1}{2}$(n≥2,n∈N).
(3)当n≥2时,${a_n}=\frac{n-1}{2}$,${T_n}={a_1}+{a_2}+{a_3}+…+{a_n}=\frac{1}{2}+\frac{1}{4}n(n-1)=\frac{{{n^2}-n+2}}{4}$,
由Tn>λ(Sn+1+1),得$\frac{{{n^2}-n+2}}{4}>λ\frac{n+2}{2}$,
∴$λ<\frac{{{n^2}-n+2}}{2(n+2)}$对任意n≥2,n∈N*都成立,
$\frac{{{n^2}-n+2}}{2(n+2)}=\frac{1}{2}[(n+2)+\frac{8}{n+2}-5]≥\frac{1}{2}(4+\frac{8}{4}-5)=\frac{1}{2}$,
当且仅当n=2时等号成立,
∴$λ<\frac{1}{2}$.
当n=1时,λ<$\frac{1}{3}$,
综上可知$λ<\frac{1}{2}$.
故λ的取值范围是(-∞,$\frac{1}{2}$).
点评 本题考查数列的前n项和,涉及了向量的中点坐标公式、采用倒序相加法求前n项和及不等式的性质,考查分析问题及解决问题得能力,综合能力强,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上的一点,BD∥平面AC1E;
如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上的一点,BD∥平面AC1E;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
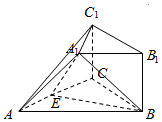 在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.
在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2004 | B. | 2006 | C. | 4008 | D. | 6011 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com