
分析 利用两点的连线的斜率公式得出kn,再利用构造辅助函数,利用函数单调性求得函数的最小值,根据等差数列前n项和公式,即可证明不等式成立.
解答 解:证明:由题意可知线段PnPn+1的斜率为kn,kn=$\frac{ln(n+1)-lnn}{n+1-n}$=ln(1+$\frac{1}{n}$),
构造辅助函数g(x)=lnx-$\frac{2(x-1)}{x+1}$(x≥1),
f′(x)=$\frac{1}{x}$-$\frac{2(x+1)-2(x+1)}{(x+1)^{2}}$=$\frac{(x-1)^{2}}{x(x+1)^{2}}$≥0,
∴f(x)在(1,+∞)单调递增,故f(x)的最小值是f(1)=0,
∴lnx>$\frac{2(x-1)}{x+1}$,
∴ln(1+$\frac{1}{n}$)>$\frac{2(1+\frac{1}{n}-1)}{1+\frac{1}{n}+1}$=$\frac{2}{2n+1}$,
∴$\frac{1}{{k}_{n}}$<$\frac{2n+1}{2}$,
$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$+…+$\frac{1}{{k}_{n}}$<$\frac{1}{2}$($\frac{(3+2n+1)n}{2}$)=$\frac{n(n+2)}{2}$,
因此:$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$+…+$\frac{1}{{k}_{n}}$<$\frac{n(n+2)}{2}$.
点评 本题考查导数的性质的综合运用及运用导数法证明函数与不等式及等差数列的综合问题的处理能力,解题时注意转化思想的运用,属于中档题.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 5 | C. | $\sqrt{10}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
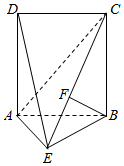 如图,平面ABCD⊥平面ABE,四边形ABCD是边长为2的正方形,且点B在平面ACE上的射影F恰好落在边CE上.
如图,平面ABCD⊥平面ABE,四边形ABCD是边长为2的正方形,且点B在平面ACE上的射影F恰好落在边CE上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
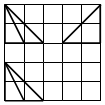 如图,网格纸上小正方形的边长为l,粗线画出的是某多面体的三视图,则该几何体的各个面中最大面的面积为( )
如图,网格纸上小正方形的边长为l,粗线画出的是某多面体的三视图,则该几何体的各个面中最大面的面积为( )| A. | l | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一锥体的三视图如图所示,则该棱锥的最长棱的棱长为( )
一锥体的三视图如图所示,则该棱锥的最长棱的棱长为( )| A. | $\sqrt{33}$ | B. | $\sqrt{17}$ | C. | $\sqrt{41}$ | D. | $\sqrt{42}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com