
分析 (Ⅰ)根据三角形的面积公式和向量数量积的计算公式便可得出$1≤tanx≤\sqrt{3}$,根据x为三角形ABC的内角及正切函数的符号即可求出x的取值范围;
(Ⅱ)根据条件及二倍角的正余弦公式和两角和的正弦公式即可得出f(x)=$2sin(2x+\frac{π}{6})+1$,这样可求出2x+$\frac{π}{6}$的范围,从而根据正弦函数的单调性即可得出函数f(x)的最大值、最小值.
解答 解:(Ⅰ)∵∠BAC=x,$\overrightarrow{AB}•\overrightarrow{AC}=8$,$4≤{S}_{△ABC}≤4\sqrt{3}$;
又${S}_{△ABC}=\frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|sin∠BAC$,
∴$\overrightarrow{AB}•\overrightarrow{AC}=|\overrightarrow{AB}||\overrightarrow{AC}|cosx=8$,S△ABC=4tanx,
即$1≤tanx≤\sqrt{3}$,
所求的x的取值范围是{x|$\frac{π}{4}≤x≤\frac{π}{3}$};
(Ⅱ)∵$\frac{π}{4}≤x≤\frac{π}{3}$,又$f(x)=2\sqrt{3}si{n}^{2}(x+\frac{π}{4})+2co{s}^{2}x-\sqrt{3}$
=$\sqrt{3}sin2x+cos2x+1$
=$2sin(2x+\frac{π}{6})+1$,
由于$\frac{2π}{3}≤2x+\frac{π}{6}≤\frac{5π}{6}$,所以$\frac{1}{2}≤sin(2x+\frac{π}{6})≤\frac{\sqrt{3}}{2}$.
∴$f(x)_{min}=f(\frac{π}{3})=2$,$f(x)_{max}=f(\frac{π}{4})=\sqrt{3}+1$.
点评 考查三角形的面积公式,向量数量积的计算公式,切化弦公式,以及两角和的正弦公式,二倍角的正余弦公式,正弦函数的图象及其单调性,函数最值的求法.


科目:高中数学 来源: 题型:选择题
 如图,棱长为4的正方体ABCD-A1B1C1D1,点A在平面α内,平面ABCD与平面α所成的二面角为30°,则顶点C1到平面α的距离的最大值是( )
如图,棱长为4的正方体ABCD-A1B1C1D1,点A在平面α内,平面ABCD与平面α所成的二面角为30°,则顶点C1到平面α的距离的最大值是( )| A. | 2(2+$\sqrt{2}$) | B. | 2($\sqrt{3}$+$\sqrt{2}$) | C. | 2($\sqrt{3}$+1) | D. | 2($\sqrt{2}$+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
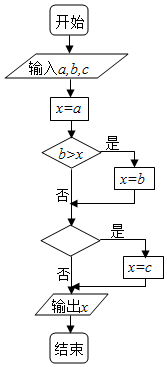 执行如图的程序框图,则判断框可填入和输出的结果分别是( )
执行如图的程序框图,则判断框可填入和输出的结果分别是( )| A. | c>x;a,b,c中最小的 | B. | c=x;a,b,c中最小的 | ||
| C. | c<x;a,b,c中最大的 | D. | c>x;a,b,c中最大的 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{8}{15}$ | D. | $\frac{7}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,2] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com