考点:棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)由已知条件推导出C
1F⊥DF,Rt△BDF≌Rt△B
1FC
1,由此推导出
=2.
(2)在平面A
1B
1C
1中,过C
1作C
1G⊥A
1B
1于G,连FG,则∠C
1FG就是C
1F与侧面AA
1B
1B所成的角,由此能求出三棱柱的体积.
解答:
(1)∵对于AD上任意一点总有EF⊥FC
1,
∴C
1F⊥平面ADF,
∴C
1F⊥DF,
∵D为BC的中点,且BF=2BD,
∴BF=B
1C
1,∠B
1FC
1=∠BDF,∠FB
1C
1=∠DBF,
∴Rt△BDF≌Rt△B
1FC
1,
∴B
1F=BD=
BF,∴
=2.(6分)
(2)在平面A
1B
1C
1中,过C
1作C
1G⊥A
1B
1于G,连FG,
则∠C
1FG就是C
1F与侧面AA
1B
1B所成的角,(8分)
则有
=
,C
1G=
C
1F,
△A
1B
1C
1中,取B
1C
1的中点D
1,连A
1D
1,
设B
1F=x,由C
1G•A
1B
1=B
1C
1•A
1D
1,
解得x=1,∴BB
1=3,(10分)
∴三棱柱的体积V=
B
1G•A
1D
1•BB
1=6
.(12分)
点评:本题考查满足条件的线段的比值的求法,考查三飘棱锥的体积的求法,解题时要认真审题,注意空间思维能力的合理运用.

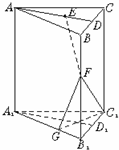
 如图,已知直三棱柱ABC-A1B1C1,AB=AC,F为BB1上一点,D为BC的中点,且BF=2BD.
如图,已知直三棱柱ABC-A1B1C1,AB=AC,F为BB1上一点,D为BC的中点,且BF=2BD. (1)∵对于AD上任意一点总有EF⊥FC1,
(1)∵对于AD上任意一点总有EF⊥FC1,

 如图,平面内的两条相交直线OP1和OP2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ
如图,平面内的两条相交直线OP1和OP2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ