
| A. | y=cosx | B. | y=-x2+2x | C. | $y={log_{\frac{1}{2}}}(x-1)$ | D. | y=e-x |
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
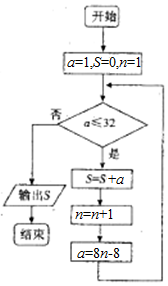 我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )
我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )| A. | 121 | B. | 81 | C. | 74 | D. | 49 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.
如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 保留 | 不支持 | |
| 30岁以下 | 900 | 120 | 280 |
| 30岁以上(含30岁) | 300 | 260 | 140 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
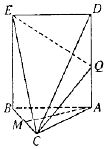 如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点
如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com