
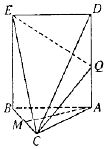
 如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点
如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点分析 (Ⅰ)推导出BE⊥AM,BC⊥AM,由此能证明AM⊥平面BEC.
(Ⅱ)由VB-ACE=VE-ABC,能求出三棱锥B-ACE的体积.
(Ⅲ)在平面QEC内作QN⊥EC,QN交CE于点N.QN与AM共面,设该平面为a,推导出四边形AMNQ是平行四方形,由此能求出AQ.
解答 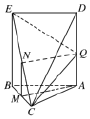 证明:(Ⅰ)∵平面ABED⊥平面ABC,平面ABED∩平面ABC=AB,
证明:(Ⅰ)∵平面ABED⊥平面ABC,平面ABED∩平面ABC=AB,
BE⊥AB,BE?平面ABED,
∴BE⊥平面ABC,又AM?平面ABC,∴BE⊥AM.
又AB=AC,M是BC的中点,∴BC⊥AM,
又BC∩BE=B,BC?平面BEC,BE?平面BEC,
∴AM⊥平面BEC.
解:(Ⅱ)由(Ⅰ)知,BE⊥平面ABC,∴h=BE=6.
在Rt△ABM中,$AM=\sqrt{A{B^2}-B{M^2}}=\sqrt{{5^2}-{3^2}}=4$,
又${S_{△ABC}}=\frac{1}{2}×BC×AM=\frac{1}{2}×6×4=12$,
∴${V_{B-ACE}}={V_{E-ABC}}=\frac{1}{3}×{S_{△ABC}}×h=\frac{1}{3}×12×6=24$.
(Ⅲ)在平面QEC内作QN⊥EC,QN交CE于点N.
∵平面QEC⊥平面BEC,平面QEC∩平面BEC-EC,
∴QN⊥平面BEC,又AM⊥平面BEC.∴QN∥AM.
∴QN与AM共面,设该平面为a,∵ABED是长方形,∴AQ∥BE,
又Q?平面BEC,BE?平面BEC,∴AQ∥平面BEC,
又AQ?α,α∩平面BEC=MN,∴AQ∥MN,又QN∥AM,
∴四边形AMNQ是平行四方形.∴AQ=MN.
∵AQ∥BE,AQ∥MN,∴MN∥BE,又M是BC的中点.∴$MN=\frac{1}{2}BE=3$,
∴AQ=MN=3.
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,考查线段长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
 如图1,已知矩形ABCD中,AB=2,$BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.
如图1,已知矩形ABCD中,AB=2,$BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{13}$ | B. | -$\frac{12}{13}$ | C. | $\frac{12}{5}$ | D. | -$\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cosx | B. | y=-x2+2x | C. | $y={log_{\frac{1}{2}}}(x-1)$ | D. | y=e-x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (0,2] | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 甲、乙两家商场对同一种商品展开促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示转盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为$\frac{π}{4}$,边界忽略不计)即为中奖.乙商场:从装有4个白球,4个红球和4个篮球的盒子中一次性摸出3球(这些球初颜色外完全相同),如果摸到的是3个不同颜色的球,即为中奖.
甲、乙两家商场对同一种商品展开促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示转盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为$\frac{π}{4}$,边界忽略不计)即为中奖.乙商场:从装有4个白球,4个红球和4个篮球的盒子中一次性摸出3球(这些球初颜色外完全相同),如果摸到的是3个不同颜色的球,即为中奖.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com