
 甲、乙两家商场对同一种商品展开促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示转盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为$\frac{π}{4}$,边界忽略不计)即为中奖.乙商场:从装有4个白球,4个红球和4个篮球的盒子中一次性摸出3球(这些球初颜色外完全相同),如果摸到的是3个不同颜色的球,即为中奖.
甲、乙两家商场对同一种商品展开促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示转盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为$\frac{π}{4}$,边界忽略不计)即为中奖.乙商场:从装有4个白球,4个红球和4个篮球的盒子中一次性摸出3球(这些球初颜色外完全相同),如果摸到的是3个不同颜色的球,即为中奖.分析 (I)利用几何概率计算公式即可得出.
(II)利用超几何分布列的性质即可得出.
解答 解:(I)设顾客去甲商场转动圆盘,指针指向阴影部分为事件A,
食言的全部结果构成的区域为圆盘,面积为πr2(r为圆盘的半径),阴影区域的面积为$S=\frac{{\frac{π}{4}×2}}{2π}π{r^2}=\frac{1}{4}π{r^2}$.
所以$P(A)=\frac{{\frac{1}{4}π{r^2}}}{{π{r^2}}}=\frac{1}{4}$,
设顾客去乙商场一次摸出3个不同颜色的球为事件B,则一切等可能得结果有$C_{12}^1=220$种;
所以$P(B)=\frac{54}{220}=\frac{16}{55}$.
因为P(A)<P(B),所以顾客在乙商场中奖的可能性大些.
(Ⅱ)由题意知,X的取值为0,1,2,3.
则$P({X=0})=\frac{C_4^0C_8^3}{{C_{12}^3}}=\frac{12}{55}$,P(X=1)=$\frac{{∁}_{4}^{1}{∁}_{8}^{2}}{{∁}_{12}^{3}}$=$\frac{28}{55}$,$P({X=2})=\frac{C_4^2C_8^1}{{C_{12}^3}}=\frac{12}{55}$,$P({X=3})=\frac{C_4^3}{{C_{12}^3}}=\frac{1}{55}$,
所以X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{14}{55}$ | $\frac{28}{55}$ | $\frac{12}{55}$ | $\frac{1}{55}$ |
点评 本题考查了几何概率计算公式、超几何分布列的性质及其数学期望计算公式,考查了推理能力与计算能力,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2人 | B. | 3人 | C. | 2人或3人 | D. | 4人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 保留 | 不支持 | |
| 30岁以下 | 900 | 120 | 280 |
| 30岁以上(含30岁) | 300 | 260 | 140 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
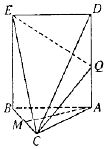 如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点
如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{63}{32}$ | B. | $\frac{31}{16}$ | C. | $\frac{123}{64}$ | D. | $\frac{127}{128}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com