
 如图1,已知矩形ABCD中,AB=2,$BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.
如图1,已知矩形ABCD中,AB=2,$BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.分析 (Ⅰ)在已知平面图形中通过求解直角三角形可得AC⊥DE,得到D'H⊥AC.再求解直角三角形证得D'H⊥HE,结合线面垂直的判定可得D'H⊥平面ABC;
(Ⅱ)由VB-AED′=VD′-ABE=$\frac{1}{3}{S}_{△ABE}×D′H$求得三棱锥B-AED'的体积.
解答 (Ⅰ)证明:在矩形ABCD中,
∵AB=2,$BC=2\sqrt{3}$,$CE=\frac{1}{3}CB$=$\frac{2\sqrt{3}}{3}$,
∴$tan∠EDC=\frac{CE}{CD}=\frac{{\sqrt{3}}}{3}$,tan∠ECH=$\frac{AB}{BC}=\frac{\sqrt{3}}{3}$,
则tan∠EDC=∠ACB.
又∵$∠DCA+∠ACB=\frac{π}{2}$,
∴$∠EDC+∠DCA=\frac{π}{2}$,
则$∠DHC=\frac{π}{2}$,
∴AC⊥DE,即D'H⊥AC.
又△CHE∽△AHD,且$\frac{CE}{AD}=\frac{1}{3}$,
∴$D'H=DH=\frac{3}{4}DE=\frac{3}{4}×\sqrt{4+\frac{4}{3}}=\frac{3}{4}$×$\frac{{4\sqrt{3}}}{3}=\sqrt{3}$.
$HE=\frac{1}{4}DE=\frac{1}{4}×\frac{{4\sqrt{3}}}{3}=\frac{{\sqrt{3}}}{3}$.
则$D'{H^2}+H{E^2}=\frac{10}{3}=D'{E^2}$.
D'H⊥HE.而直线AC与HE是平面ABC内的两条相交直线,
∴D'H⊥平面ABC;
(Ⅱ)由(Ⅰ)知,D'H⊥平面ABC,且$D'H=\sqrt{3}$.
∴VB-AED′=VD′-ABE=$\frac{1}{3}{S}_{△ABE}×D′H$=$\frac{1}{3}×\frac{1}{2}×AB×BE×D′H$=$\frac{1}{6}×2×(\frac{2}{3}×2\sqrt{3})×\sqrt{3}$=$\frac{4}{3}$.
点评 本题考查线面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,在平面图形中证得AC⊥DE是解答该题的关键,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | -$\frac{1}{8}$ | C. | 8 | D. | -8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [(k+$\frac{1}{2}$)π,(k+1)π] | B. | [(2k+1)π,2(k+1)π] | C. | [kπ,(k+$\frac{1}{2}$)π] | D. | [2kπ,(2k+1)π] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
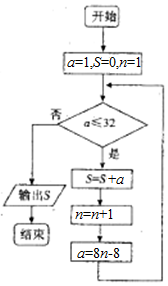 我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )
我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )| A. | 121 | B. | 81 | C. | 74 | D. | 49 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2人 | B. | 3人 | C. | 2人或3人 | D. | 4人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
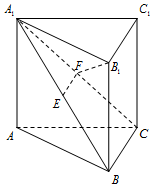 如图,在直三棱柱ABC-A1B1C1中,A1B1⊥B1C1,E、F分别是A1B、A1C的中点.
如图,在直三棱柱ABC-A1B1C1中,A1B1⊥B1C1,E、F分别是A1B、A1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
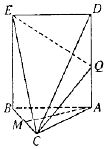 如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点
如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com