
分析 (Ⅰ)由已知及正弦定理,得$\sqrt{3}sinBsinA=sinAcosB$,结合sinA≠0,可求$tanB=\frac{{\sqrt{3}}}{3}$,由于0<B<π,可求B的值.
(Ⅱ)由已知及正弦定理,得$c=\sqrt{3}a$,利用余弦定理可求${a^2}+{c^2}-\sqrt{3}ac=9$,联立即可解得a,c的值.
解答 解:(Ⅰ)由$\sqrt{3}bsinA=acosB$及正弦定理,得$\sqrt{3}sinBsinA=sinAcosB$.
在△ABC中,sinA≠0,∴$\sqrt{3}sinB=cosB$,∴$tanB=\frac{{\sqrt{3}}}{3}$.
∵0<B<π,
∴$B=\frac{π}{6}$.
(Ⅱ)由$sinC=\sqrt{3}sinA$及正弦定理,得$c=\sqrt{3}a$,①
由余弦定理b2=a2+c2-2accosB得,${3^2}={a^2}+{c^2}-2accos\frac{π}{6}$,
即${a^2}+{c^2}-\sqrt{3}ac=9$,②
由①②,解得$a=3,c=3\sqrt{3}$.
点评 本题主要考查了正弦定理,余弦定理,同角三角函数基本关系式在解三角形中的应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:解答题
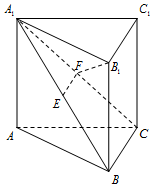 如图,在直三棱柱ABC-A1B1C1中,A1B1⊥B1C1,E、F分别是A1B、A1C的中点.
如图,在直三棱柱ABC-A1B1C1中,A1B1⊥B1C1,E、F分别是A1B、A1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.
如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
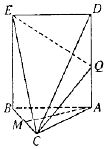 如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点
如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{27}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2loga8 | B. | 16 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
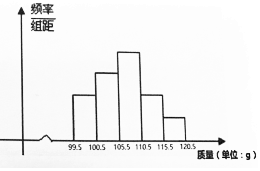 检测600个某产品的质量(单位:g),得到的直方图中,前三组的长方形的高度成等差数列,后三组对应的长方形的高度成公比为0.5的等比数列,已知检测的质量在100.5-105.5之间的产品数为150,则质量在115.5-120.5的长方形高度为( )
检测600个某产品的质量(单位:g),得到的直方图中,前三组的长方形的高度成等差数列,后三组对应的长方形的高度成公比为0.5的等比数列,已知检测的质量在100.5-105.5之间的产品数为150,则质量在115.5-120.5的长方形高度为( )| A. | $\frac{1}{12}$ | B. | $\frac{1}{30}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{60}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com