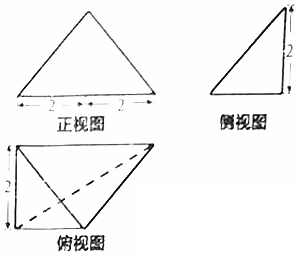
某四面体的三视图如图所示.则其四个面中最大面的面积是( )A．4B．$2\sqrt{2}$C．$2\sqrt{6}$D．$4\sqrt{2}$ 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

18．某四面体的三视图如图所示，则其四个面中最大面的面积是（　　）

A．

B．

$2\sqrt{2}$

C．

$2\sqrt{6}$

D．

$4\sqrt{2}$

分析由三视图可知：该几何体为三棱锥PABC，AC⊥CB．过点P作PO⊥底面ABC，垂足为O．连接OA，则OA∥BC，OA=$\frac{1}{2}$BC．

解答解：由三视图可知：该几何体为三棱锥PABC，AC⊥CB．过点P作PO⊥底面ABC，垂足为O．
连接OA，则OA∥BC，OA=$\frac{1}{2}$BC．
∴最大面积为△PBC，其面积S=$\frac{1}{2}×4×\sqrt{{2}^{2}+{2}^{2}}$=$4\sqrt{2}$．
故选：D．

点评本题考查了三棱锥的三视图、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

12．已知双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$上有不共线三点A，B，C，且AB，BC，AC的中点分别为D，E，F，若满足OD，OE，OF的斜率之和为-1，则$\frac{1}{{{k_{AB}}}}+\frac{1}{{{k_{BC}}}}+\frac{1}{{{k_{AC}}}}$=（　　）

A．

B．

$-\sqrt{3}$

C．

-2

D．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

9．在△ABC中，角A，B，C所对的边分别为a，b，c，若sinA=$\frac{2}{3}$，sinB=2cosC且c²-a²=b，则b=3．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．在二项式（x+$\frac{1}{2•\root{3}{x}}$）ⁿ的展开式中，若前三项系数成等差数列，则展开式中的常数项为（　　）

A．

$\frac{7}{16}$

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

13．设a_n=xⁿ，b_n=（$\frac{1}{n}$）²，S_n为数列{a_n•b_n}的前n项和，令f_n（x）=S_n-1，x∈R，a∈N^*．
（Ⅰ）若x=2，求数列{$\frac{2n-1}{{a}_{n}}$}的前n项和T_n；
（Ⅱ）求证：对?n∈N^*，方程f_n（x）=0在x_n∈[$\frac{2}{3}$，1]上有且仅有一个根；
（Ⅲ）求证：对?p∈N^*，由（Ⅱ）中x_n构成的数列{x_n}满足0＜x_n-x_n+p＜$\frac{1}{n}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

3．

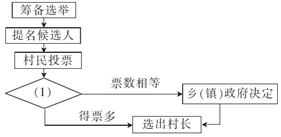选举时常用的选举方式是差额选举（候选人多于当选人数），某村选举村长，具体方法是：筹备选举，由乡（镇）政府提名候选人，村民投票（同意，不同意，弃权），验票统计，得票多者选为村长；若票数相等，则由乡（镇）政府决定谁当选．下面的流程图表示该选举过程，则图（1）处应填的是验票统计．