
分析 (Ⅰ)$\frac{2n-1}{{a}_{n}}$=(2n-1)($\frac{1}{2}$)n,利用“错位相减法”即可求得数列{$\frac{2n-1}{{a}_{n}}$}的前n项和Tn;
(Ⅱ)由题意可得f′(x)>0,函数f(x)在(0,+∞)上是增函数.求得fn(1)>0,fn($\frac{2}{3}$)<0,再根据函数的零点的判定定理,可得要证的结论成立.
(Ⅲ)由题意可得fn+1(xn)>fn(xn)=fn+1(xn+1)=0,由 fn+1(x) 在(0,+∞)上单调递增,可得 xn+1<xn,故xn-xn+p>0.用 fn(x)的解析式减去fn+p (xn+p)的解析式,变形可得xn-xn+p=$\sum_{k=2}^{n}$$\frac{{x}_{n+p}^{k}-{x}_{n}^{k}}{{k}^{2}}$+$\sum_{k=n+1}^{n+p}$$\frac{{x}_{n+p}^{k}}{{k}^{2}}$,再进行放大,并裂项求和,可得它小于$\frac{1}{n}$.,综上可得要证的结论成立.
解答 解:(Ⅰ)若x=2,an=2n,则$\frac{2n-1}{{a}_{n}}$=(2n-1)($\frac{1}{2}$)n,
则Tn=1×($\frac{1}{2}$)1+3×($\frac{1}{2}$)2+…+(2n-1)($\frac{1}{2}$)n,
∴$\frac{1}{2}$Tn=1×($\frac{1}{2}$)2+3×($\frac{1}{2}$)3+…+(2n-1)($\frac{1}{2}$)n+1,
∴$\frac{1}{2}$Tn=$\frac{1}{2}$+2×[($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)n]-(2n-1)($\frac{1}{2}$)n+1
=$\frac{1}{2}$+2×$\frac{\frac{1}{4}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$-(2n-1)($\frac{1}{2}$)n+1=$\frac{1}{2}$+1-($\frac{1}{2}$)n-1-(2n-1)($\frac{1}{2}$)n+1,
∴Tn=3-($\frac{1}{2}$)n-2-(2n-1)($\frac{1}{2}$)n=3-$\frac{2n+3}{{2}^{n}}$;
(Ⅱ)证明:fn(x)=-1+x+$\frac{{x}^{2}}{{2}^{2}}$+$\frac{{x}^{3}}{{3}^{2}}$+…+$\frac{{x}^{n}}{{n}^{2}}$(x∈R,n∈N+),fn′(x)=1+$\frac{x}{2}$+$\frac{{x}^{2}}{3}$+…+$\frac{{x}^{n-1}}{n}$>0,
故函数f(x)在(0,+∞)上是增函数.
由于f1(x1)=0,当n≥2时,fn(1)=$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$>0,即fn(1)>0.
又fn($\frac{2}{3}$)=-1+$\frac{2}{3}$+[$\frac{(\frac{2}{3})^{2}}{{2}^{2}}$+$\frac{(\frac{2}{3})^{2}}{{3}^{2}}$+$\frac{(\frac{2}{3})^{4}}{{4}^{2}}$+…+$\frac{(\frac{2}{3})^{n}}{{n}^{2}}$]≤-$\frac{1}{3}$+$\frac{1}{4}$•$\sum_{i=2}^{n}$($\frac{2}{3}$)i,
=-$\frac{1}{3}$+$\frac{1}{4}$×$\frac{(\frac{2}{3})^{2}[1-(\frac{2}{3})^{n-1}]}{1-\frac{2}{3}}$=-$\frac{1}{3}$•($\frac{2}{3}$)n-1<0,
根据函数的零点的判定定理,可得存在唯一的xn∈[$\frac{2}{3}$,1],满足fn(xn)=0.
(Ⅲ)证明:对于任意p∈N+,由(1)中xn构成数列{xn},当x>0时,
∵fn+1(x)=fn(x)+$\frac{{x}^{n+1}}{(n+1)^{2}}$>fn(x),
∴fn+1(xn)>fn(xn)=fn+1(xn+1)=0.
由 fn+1(x) 在(0,+∞)上单调递增,可得 xn+1<xn,即 xn-xn+1>0,
故数列{xn}为减数列,即对任意的 n、p∈N+,xn-xn+p>0.
由于 fn(xn)=-1+xn+$\frac{{x}_{n}^{2}}{{2}^{2}}$+$\frac{{x}_{n}^{3}}{{3}^{2}}$+…+$\frac{{x}_{n}^{n}}{{n}^{2}}$=0,①,
fn+p (xn+p)=-1+xn+p+$\frac{{x}_{n+p}^{2}}{{3}^{2}}$+$\frac{{x}_{n+p}^{3}}{{3}^{2}}$+…+$\frac{{x}_{n+p}^{n}}{{n}^{2}}$+[$\frac{{x}_{n+p}^{n+1}}{(n+1)^{2}}$+$\frac{{x}_{n+p}^{n+2}}{(n+2)^{2}}$+…+$\frac{{x}_{n+p}^{n+p}}{(n+p)^{2}}$],②,
用①减去②并移项,利用 0<xn+p≤1,可得
xn-xn+p=$\sum_{k=2}^{n}$$\frac{{x}_{n+p}^{k}-{x}_{n}^{k}}{{k}^{2}}$+$\sum_{k=n+1}^{n+p}$$\frac{{x}_{n+p}^{k}}{{k}^{2}}$≤$\sum_{k=n+1}^{n+p}$$\frac{{x}_{n+p}^{k}}{{k}^{2}}$≤$\sum_{k=n+1}^{n+p}$$\frac{1}{{k}^{2}}$<$\sum_{k=n+1}^{n+p}$$\frac{1}{k(k-1)}$=$\frac{1}{n}$-$\frac{1}{n+p}$<$\frac{1}{n}$.
综上可得,对于任意p∈N+,由(1)中xn构成数列{xn}满足0<xn-xn+p<$\frac{1}{n}$.
点评 本题主要考查函数的导数及应用,函数的零点的判定,等比数列求和以及用放缩法证明不等式,“错位相减法”求数列的前n项和,还考查推理以及运算求解能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|1≤x<2} | C. | {x|-1<x<2} | D. | {x|-1≤x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2$\sqrt{5}$,-4] | B. | (-2$\sqrt{5}$,-4] | C. | [-2$\sqrt{5}$,-4) | D. | (-2$\sqrt{5}$,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
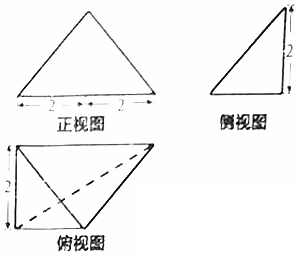
| A. | 4 | B. | $2\sqrt{2}$ | C. | $2\sqrt{6}$ | D. | $4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com