
分析 a>0时,f(x)=$\left\{\begin{array}{l}{(x-\frac{a}{2})^{2}-\frac{{a}^{2}}{4},x≥0}\\{-(x-\frac{a}{2})^{2}+\frac{{a}^{2}}{4},x<0}\end{array}\right.$,利用单调性即可判断出不存在反函数.
a=0时,f(x)=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{-{x}^{2},x<0}\end{array}\right.$,可得函数f(x)在R上单调递增,因此存在反函数.
a<0时,f(x)=$\left\{\begin{array}{l}{(x-\frac{a}{2})^{2}-\frac{{a}^{2}}{4},x≥0}\\{-(x-\frac{a}{2})^{2}+\frac{{a}^{2}}{4},x<0}\end{array}\right.$,利用单调性即可判断出不存在反函数.
解答 解:a>0时,f(x)=$\left\{\begin{array}{l}{(x-\frac{a}{2})^{2}-\frac{{a}^{2}}{4},x≥0}\\{-(x-\frac{a}{2})^{2}+\frac{{a}^{2}}{4},x<0}\end{array}\right.$,
可得函数f(x)在$(0,\frac{a}{2})$内单调递减,在(-∞,0),$(\frac{a}{2},+∞)$上单调递增,因此不存在反函数.
a=0时,f(x)=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{-{x}^{2},x<0}\end{array}\right.$,可得函数f(x)在(-∞,+∞)上单调递增,因此存在反函数.
a<0时,f(x)=$\left\{\begin{array}{l}{(x-\frac{a}{2})^{2}-\frac{{a}^{2}}{4},x≥0}\\{-(x-\frac{a}{2})^{2}+\frac{{a}^{2}}{4},x<0}\end{array}\right.$,
可得函数f(x)在$(\frac{a}{2},0)$内单调递减,在(-∞,$\frac{a}{2}$),(0,+∞)上单调递增,
因此不存在反函数.
综上可得:a=0.
故答案为:0.
点评 本题考查了反函数的定义及其判定、二次函数的单调性、分类讨论方法,考查了推理能力与计算能力,属于中档题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | 有最大值$\frac{{e}^{2}}{8}$ | B. | 有最小值$\frac{{e}^{2}}{8}$ | C. | 有最大值$\frac{{e}^{2}}{2}$ | D. | 有最小值$\frac{{e}^{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |x-y|<2t | B. | |x-y|<t | C. | |x-y|>2t | D. | |x-y|>t |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.
如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
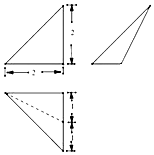
| A. | $2\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
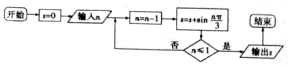
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com