
| A. | -84 | B. | 84 | C. | -36 | D. | 36 |
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.
如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
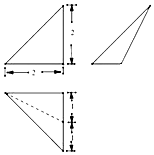
| A. | $2\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | ±1 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
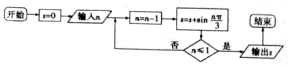
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com