
【题目】已知函数f(x)=x2+ax+b﹣a(a,b∈R).
(1)若关于x的不等式f(x)>0的解集为(﹣∞,﹣1)∪(3,+∞),求实数a,b的值;
(2)设a=2,若不等式f(x)>b2﹣3b对任意实数x都成立,求实数b的取值范围;
(3)设b=3,解关于x的不等式组 ![]() .
.
【答案】
(1)解:因为不等式f(x)=x2+ax+b﹣a>0的解集为(﹣∞,﹣1)∪(3,+∞),
所以由题意得﹣1,3为函数x2+ax+b﹣a=0的两个根,
所以 ![]() ,解得a=﹣2,b=﹣5
,解得a=﹣2,b=﹣5
(2)解:当a=2时,x2+2x+b﹣2>b2﹣3b恒成立,即x2+2x﹣2>b2﹣4b恒成立.
因为x2+2x﹣2=(x+1)2﹣3≥﹣3,所以b2﹣4b<﹣3,
解之得1<b<3,所以实数b的取值范围为1<b<3
(3)当b=3时,f(x)=x2+ax+3﹣a,f(x)的图象的对称轴为 ![]() .
.
(ⅰ)当△<0,即﹣6<a<2时,由 ![]() ,得x>1,
,得x>1,
(ⅱ)当△=0,即a=2或﹣6时
①当a=2时,由 ![]() ,得
,得 ![]() ,所以x>1,
,所以x>1,
②当a=﹣6时,由 ![]() ,得
,得 ![]() ,所以1<x<3或x>3,
,所以1<x<3或x>3,
(ⅲ)当△>0,即a<﹣6或a>2时,方程f(x)=0的两个根为 ![]() ,
, ![]() ,
,
①当a<﹣6时,由 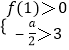 知1<x1<x2,所以
知1<x1<x2,所以 ![]() 的解为1<x<x1或x>x2,
的解为1<x<x1或x>x2,
②当a>2时,由 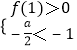 知x1<x2<1,所以
知x1<x2<1,所以 ![]() 的解为x>1,
的解为x>1,
综上所述,
当a≤﹣6时,不等式组的解集为 ![]() ,
,
当a>﹣6时,不等式组的解集为(1,+∞)
【解析】(1)把问题转化为一元二次方程的问题,利用方程的根建立二次一次方程组,求得a和b的值.(2)把不等式整理成x2+2x﹣2>b2﹣4b确定等号左边的最小值,进而确定等号右边的范围求得b的范围.(3)对判别式△大于0和小于0进行分类讨论,通过解不等式求得解集.
【考点精析】认真审题,首先需要了解二次函数的性质(当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减).
上递减).


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
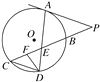
【题目】如图所示,已知PA与⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD,BC相交于E点,F为CE上一点,且DE2=EF·EC.
(1)求证:∠P=∠EDF;
(2)求证:CE·EB=EF·EP;
(3)若CE∶BE=3∶2,DE=6,EF=4,求PA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ) ![]() 的最小正周期为π,
的最小正周期为π,
(1)求当f(x)为偶函数时φ的值;
(2)若f(x)的图象过点( ![]() ,
, ![]() ),求f(x)的单调递增区间.
),求f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知角α的顶点在坐标原点,始边与x轴的非负半轴重合,终边经过点 ![]() .
.
(1)求sin2α﹣tanα的值;
(2)若函数f(x)=cos(x﹣α)cosα﹣sin(x﹣α)sinα,求函数 ![]() 在区间
在区间 ![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3﹣2ex2+mx﹣lnx,记g(x)= ![]() ,若函数g(x)至少存在一个零点,则实数m的取值范围是( )
,若函数g(x)至少存在一个零点,则实数m的取值范围是( )
A.(﹣∞,e2+ ![]() ]
]
B.(0,e2+ ![]() ]
]
C.(e2+ ![]() ,+∞]
,+∞]
D.(﹣e2﹣ ![]() ,e2+
,e2+ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个四棱锥的三视图如图所示,关于这个四棱锥,下列说法正确的是( )

A. 最长的棱长为![]()
B. 该四棱锥的体积为![]()
C. 侧面四个三角形都是直角三角形
D. 侧面三角形中有且仅有一个等腰三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com