Question

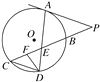
【题目】如图所示，已知PA与⊙O相切，A为切点，PBC为割线，弦CD∥AP，AD，BC相交于E点，F为CE上一点，且DE2＝EF·EC.

(1)求证：∠P＝∠EDF；

(2)求证：CE·EB＝EF·EP；

(3)若CE∶BE＝3∶2，DE＝6，EF＝4，求PA的长．

Answer 1

【答案】(1)见解析(2)见解析（3）

【解析】(1)证明 ∵DE2＝EF·EC，∴DE∶CE＝EF∶ED.

∵∠DEF是公共角，∴△DEF∽△CED.

∴∠EDF＝∠C.

∵CD∥AP，∴∠C＝∠P.

∴∠P＝∠EDF.

(2)证明　∵∠P＝∠EDF，∠DEF＝∠PEA，

∴△DEF∽△PEA.

∴DE∶PE＝EF∶EA.即EF·EP＝DE·EA.

∵AD、BC相交于点E，

∴DE·EA＝CE·EB.∴CE·EB＝EF·EP.

(3)解 ∵DE2＝EF·EC，DE＝6，EF＝4，∴EC＝9.

∵CE∶BE＝3∶2，∴BE＝6.

∵CE·EB＝EF·EP，∴9×6＝4×EP.

解得：EP＝.

∴PB＝PE－BE＝，PC＝PE＋EC＝.

由切割线定理得：PA2＝PB·PC，

∴PA2＝×，

∴PA＝ .