考点:点、线、面间的距离计算,直线与平面所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)先证明AB⊥AC,AB⊥AA1,可得AB⊥平面ACC1A1,即可证明AB⊥A1C.
(Ⅱ)直线BC1与平面ACC1A1所成的角为∠BC1A,即可求直线BC1与平面ACC1A1所成角的正切值.
(Ⅲ)利用等积变换,可求点A到平面A1BC的距离.
解答:
(Ⅰ)证明:∵△ABC中,AB=1,AC=
,∠ABC=60°,
∴由正弦定理有
=,∴sin∠ACB=
,
又AB<AC,∴∠ACB=30°.
从而∠BAC=90°,即AB⊥AC,
又直三棱柱ABC-A
1B
1C
1中,AA
1⊥平面ABC,∴AB⊥AA
1,
∴AB⊥平面ACC
1A
1,∴AB⊥A
1C …(4分)
(Ⅱ)解:∵AB⊥平面ACC
1A
1,
∴直线BC
1与平面ACC
1A
1所成的角为∠BC
1A,
在RtBC
1A中AB=1,AC
1=
=
,
∴tan∠BC
1A=
=
…(8分)
(Ⅲ)解:设点A到平面A
1BC的距离为h,则
△A
1BC中,A
1B=BC=2,A
1C=
,∴S
△A1BC=
••=
,
∴由等体积可得
•
•1•
•
=
•
h,
∴h=
…(12分)
点评:本题着重考查了直棱柱的性质、线面垂直的判定与性质和线面所成角的定义及等积变换等知识,属于中档题.

 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=

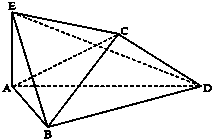 菱形ABCD边长为2,∠BAD=60°,将ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=
菱形ABCD边长为2,∠BAD=60°,将ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=