已知函数f(x)=ex+e-x(e为自然对数的底数),其导函数为f′(x),有下列四个结论:
①f′(x)的图象关于原点对称; ②f′(x)在R上不是增函数;
③f′(|x|)的图象关于y轴对称; ④f′(|x|)的最小值为0
其中正确的结论是________(填写正确结论的序号).
①③④
分析:①先求导,再利用奇函数的定义即可判断出是否是奇函数;
②对f′(x)求导,再进行判断即可;
③利用奇偶性的定义进行判断即可;
④通过换元求导即可得出.
解答:①∵函数f(x)=e
x+e
-x(e为自然对数的底数),∴f
′(x)=e
x-e
-x.
∴f
′(-x)=e
-x-e
x=-f
′(x),∴导函数f′(x)是奇函数,其图象关于原点对称,∴①正确;
②∵[f
′(x)]
′=e
x+e
-x>0,∴f′(x)在R上是增函数,故②不正确;
③∵f
′(|x|)=f
′(|-x|),∴f
′(|x|)是偶函数,其图象关于y轴对称;
④∵f
′(|x|)=e
|x|-e
-|x|,e
|x|≥e
0=1.
令e
|x|=t≥1,则f
′(|x|)=g(t)=

(t≥1).
∵
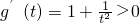
,∴函数g(t)在[1,+∞)上单调递增.
∴f
′(|x|)=g(t)≥g(1)=0,故f′(|x|)的最小值为0,即④正确.
综上可知:只有①③④正确.
故答案为①③④.
点评:熟练掌握利用导数研究函数的性质是解题的关键.

 (t≥1).
(t≥1).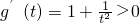 ,∴函数g(t)在[1,+∞)上单调递增.
,∴函数g(t)在[1,+∞)上单调递增.
