练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    执行下图所示的程序框图，若输入A=2014，B=125，输出的A的值是____     ．


    1      

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    函数的图象的一条对称轴方程是                     （      ）

       A．      B.         C.            D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知无穷数列{an}的各项均为正整数，Sn为数列{an}的前n项和．

    (1)若数列{an}是等差数列，且对任意正整数n都有Sn3＝(Sn)3成立，求数列{an}的通项公式；

    (2)对任意正整数n，从集合{a1，a2，…，an}中不重复地任取若干个数，这些数之间经过加减运算后所得数的绝对值为互不相同的正整数，且这些正整数与a1，a2，…，an一起恰好是1至Sn全体正整数组成的集合．

    (ⅰ)求a1，a2的值；

    (ⅱ)求数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知各项均为正数的数列{an}的前n项和为Sn，满足8Sn＝a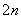＋4an＋3(n∈N*)，且a1，a2，a7依次是等比数列{bn}的前三项．

    (1)求数列{an}及{bn}的通项公式；

    (2)是否存在常数a＞0且a≠1，使得数列{an－logabn}(n∈N*)是常数列？若存在，求出a的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    第22届冬季奥运会于2014年2月7日在俄罗斯索契开幕，到冰壶比赛场馆服务的大学生志愿者中，有2名来自莫斯科国立大学，有4名来自圣彼得堡国立大学，现从这6名志愿者中随机抽取2人，至少有1名志愿者来自莫斯科国立大学的概率是（    ）

        A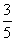．      B．       C．      D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，a、b、c分别为角A、B、C所对的边，且

    （2b+c）cosA+acosC =0

        （I）求角A的大小：

        （II）求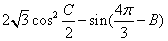的最大值，并求取得最大值时角    B．C的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设A、B是两个非空集合，定义运算，已知

      ），则A× B=（  ）

        A．[o,1]            B．[o,2]  

        C．∞）      D．[0，1] （2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知矩形ABCD中，AB=2，AD=5，E，F分别在AD，BC上且AE=1，BF=3，将四边形AEFB沿EF折起，使点B在平面CDEF上的射影H在直线DE上．

           

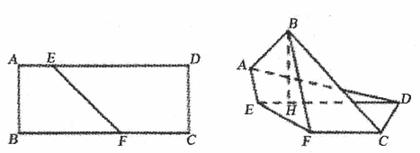
        （1）求证：AD//平面BFC；

        （2）求二面角A- DE -F的平面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图：在四棱锥中，底面是正方形，，，点在上，且.

    （Ⅰ）求证：平面；   

    （Ⅱ）求二面角的余弦值；

    （Ⅲ）证明：在线段上存在点，使∥平面，并求的长.

    查看答案和解析>>

    同步练习册答案