
已知各项均为正数的 数列{an}的前n项和为Sn,满足8Sn=a
数列{an}的前n项和为Sn,满足8Sn=a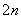 +4an+3(n∈N
+4an+3(n∈N *),且a1,a2,a7依次是等比数列{bn}的前三项.
*),且a1,a2,a7依次是等比数列{bn}的前三项.
(1)求数列{an}及{bn}的通项公式;
(2)是否存在常数a>0且a≠1,使 得数列{an-logabn}(n∈N*)是常数列?若存在,求出a的值;若不存在,说明理由.
得数列{an-logabn}(n∈N*)是常数列?若存在,求出a的值;若不存在,说明理由.
解 (1)n=1时,8a1=a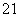 +4a1+3,a1=1或a1=3.(2分)
+4a1+3,a1=1或a1=3.(2分)
当n≥2时,8Sn-1=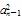 +4an-1+3,
+4an-1+3,
an=Sn-Sn-1=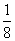 (a
(a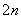 +4an-
+4an-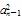 -4an-1),
-4an-1),
从而(an+an-1)(an-an-1-4)=0
因为{an}各项均为正数,所以an-an-1=4.(6分)
所以,当a1=1时,an= 4n-3;当a1=3时,an=4n-1.
4n-3;当a1=3时,an=4n-1.
又因为当a1=1时,a1,a2,a7分别为1,5,25,构成等比数列,
所以an=4n-3,bn=5n-1.
当a1=3时,a1,a2,a7分别为3,7,27,不构成等比数列, 舍去.(11分)
舍去.(11分)
(2)假设存在a,理由如下:(12分)
由(1)知,an=4n-3,bn=5n-1,从而
an-lonabn=4n-3-loga5n-1=4n-3-(n-1)·loga5=(4-loga5)n-3+loga5.
由题意,得4-loga5=0,所以a=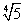 .(16分)
.(16分)


科目:高中数学 来源: 题型:
已知函数f(x)=x2-(1+2a)x+aln x(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的前三项分别为a1=5,a2=6,a3=8,且数列{an}的前n项和Sn满足Sn+m= (S2n+S2m)-(
(S2n+S2m)-( n-m)2,其中m,n为任意正整数.
n-m)2,其中m,n为任意正整数.
(1)求数列{an}的通项公式及前n项和Sn;
(2)求满足S -
-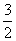 an+33=k2的所有正整数k,n.
an+33=k2的所有正整数k,n.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的通项公式为an=3n-2(n∈N+),则a3+a6 +a9+a12+a15=( )
A. 120 B. 125 C. 130 D. 135
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com