
已知函数f(x)=x2-(1+2a)x+aln x(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
解 (1)当a=-1时,f(x)=x2+x-ln x,则f′(x)=2x+1-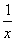 ,(2
,(2 分)
分)
所以f(1)=2,且f′(1)=2.
所以曲线y=f(x)在x=1处的切线的方程为:y-2=2(x-1),
即:y=2x.(6分)
(2)由题意得f′(x)=2x-(1+2a)+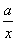 =
=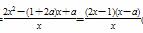 (x>0),
(x>0),
由f′(x )=0,得x1=
)=0,得x1=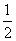 ,x2=a,(8分)
,x2=a,(8分)
①当0<a<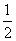 时,由f′(x)>0,又知x>0得0<x<a或
时,由f′(x)>0,又知x>0得0<x<a或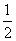 <x<1
<x<1
由f′(x)<0,又知x>0,得a<x<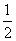 ,
,
所以函数f(x)的单调增区间是(0,a)和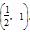 ,单调减区间是
,单调减区间是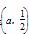 ,(10分)
,(10分)
②当a=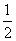 时,f′(x)=
时,f′(x)= ≥0,且仅当x=
≥0,且仅当x=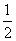 时,f′(x)=0,
时,f′(x)=0,
所以函数f(x)在区间(0,1)上是单调增函数.(11分)
③当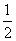 <a<1时,由f′(x)>0,又知x>0得0<x<
<a<1时,由f′(x)>0,又知x>0得0<x<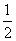
 或a<x<1,
或a<x<1,
由f′(x)<0,又知x>0,得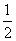 <x<a,
<x<a,
所以函数f(x)的单调增区间是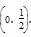 和(a,1),单调减区间是
和(a,1),单调减区间是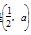 ,(13分)
,(13分)
④当a≥1时,由f′(x)>0,又知x>0得0<x<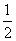 ,
,
由f′(x)<0,又知x>0,得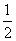 <x<1,
<x<1,
所以函数f(x)的单调增区间是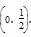 ,单调减区间是
,单调减区间是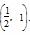 .(16分)
.(16分)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知椭圆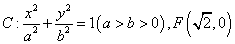 为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2
为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2
(I)求椭圆C的方程;
(II)设直线 与椭圆C相交于A、B两点,以线段OA,OB为邻边作平行四边形OAPB,其中顶点P在椭圆C上,O为坐标原点,求
与椭圆C相交于A、B两点,以线段OA,OB为邻边作平行四边形OAPB,其中顶点P在椭圆C上,O为坐标原点,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知无穷数列{an}的各项均为正整数,Sn为数列{an}的前n项和.
(1)若数列{an}是等差数列,且对任意正整数n都有Sn3=(Sn)3成立,求数列{an}的通项公式;
(2)对任意正整数n,从集合{a1,a2,…,an}中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与a1,a2,…,an一起恰好是1至Sn全体正整数组成的集合.
(ⅰ)求a1,a2的值;
(ⅱ)求 数列{an}的通项公式.
数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,椭圆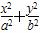 =1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直
=1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直 线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为
线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为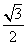 ,且过点A(0,1).
,且过点A(0,1).
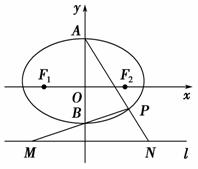
(1)求k1·k2的值;
(2)求MN的最小值;
(3)随着点P的变化,以MN为直径的圆是否恒过定点?若过定点,求出该定点;如不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知各项均为正数的 数列{an}的前n项和为Sn,满足8Sn=a
数列{an}的前n项和为Sn,满足8Sn=a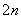 +4an+3(n∈N
+4an+3(n∈N *),且a1,a2,a7依次是等比数列{bn}的前三项.
*),且a1,a2,a7依次是等比数列{bn}的前三项.
(1)求数列{an}及{bn}的通项公式;
(2)是否存在常数a>0且a≠1,使 得数列{an-logabn}(n∈N*)是常数列?若存在,求出a的值;若不存在,说明理由.
得数列{an-logabn}(n∈N*)是常数列?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,a、b、c分别为角A、B、C所对的边,且
(2b+c)cosA+acosC =0
(I)求角A的大小:
(II)求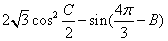 的最大值,并求取得最大值时角 B.C的大小.
的最大值,并求取得最大值时角 B.C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com