
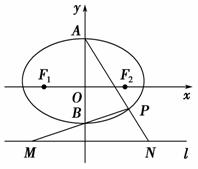
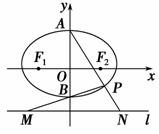
如图,椭圆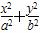 =1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直
=1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直 线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为
线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为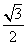 ,且过点A(0,1).
,且过点A(0,1).
(1)求k1·k2的值;
(2)求MN的最小值;
(3)随着点P的变化,以MN为直径的圆是否恒过定点?若过定点,求出该定点;如不过定点,请说明理由.
解 (1)因为e=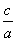 =
=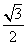 ,b=1,解得a=2,所以椭圆C的标准方程为
,b=1,解得a=2,所以椭圆C的标准方程为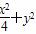 =1.(2分)
=1.(2分)
设椭圆上点P(x0,y0),有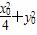 =1,
=1,
所以k1·k2=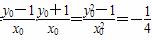 (2)因为M,N在直线l:y=-2上,设M(x1,-2),N(x2,-2),
(2)因为M,N在直线l:y=-2上,设M(x1,-2),N(x2,-2),
由方程知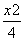 +y2=1知,A(0,1),B(0,-1),
+y2=1知,A(0,1),B(0,-1),
所以KBM·kAN=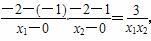 (6分)
(6分)
又由(1)知kAN·kBM=k1·k2=-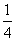 ,所以x1x2=-12,(8分)
,所以x1x2=-12,(8分)
不妨设x1<0,则x2>0,则
MN=|x1-x2|=x2-x1=x2+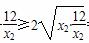 =4
=4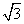 ,
,
所以当且仅当x2=-x1=2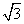 时,MN取得最小值4
时,MN取得最小值4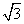 .(10分)
.(10分)
(3)设M(x1,-2),N(x2,-2),
则以MN为直径的圆的方程为
(x-x1)(x-x2)+(y+2)2=0,(12分)
即x2+(y+2)2-12-(x1+x2)x=0,若圆过定点,
则有x=0,x2+(y+2)2-12=0,解得x=0,y=-2±2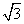 ,
,
所以,无论点P如何变化,以MN为直径的圆恒过定点(0,-2±2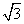 ).(16分)
).(16分)


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1: =1,A1,A2分别为椭圆C1的左、右顶点.椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”.
=1,A1,A2分别为椭圆C1的左、右顶点.椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”.
(1)求椭圆C2的方程;
(2)设P为椭圆C2上异于A1,A2的任意一点,过P作PQ⊥x轴,垂足为Q,线段PQ交椭圆C1于点H.求证:H为△PA1A2的垂心.(垂心为三角形三条高的交点)

查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x2-(1+2a)x+aln x(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
经市场调查,某旅游城市在过去的一个月内(以30天计),旅游人数f(t)(万人)与时间t(天)的函数关系近似满足f(t)=4+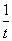 ,人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)=115-|t-15|.
,人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)=115-|t-15|.
(1)求该城市的旅游日收益w(t)(万元)与时间t(1≤t≤30,t∈N*)的函数关系式;
(2)求该城市旅游日收益的最小值(万元).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的通项公式为an=3n-2(n∈N+),则a3+a6 +a9+a12+a15=( )
A. 120 B. 125 C. 130 D. 135
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x3+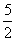 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+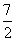 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数).
(I)若g(x)在x=l处的切线方程为y=kx-5(k为常数),求b的值;
(II)设函数f(x)的导函数为f’(x),若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
(III)令F(x)=f(x)-g(x),若函数F(x)存在极值,且所有极值之和大于5+1n2,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图4,已知三棱柱ABC—A1B1C1的侧棱与底面垂直,且∠ACB=90°,
∠BAC=30°,BC=1,AA1= ,点P、M、N分别为BC1、CC1、AB1
,点P、M、N分别为BC1、CC1、AB1
的中点.
(1)求证:PN//平面ABC;
(2)求证:AB1⊥A1M;
(3)求二面角C1—A B1—A1的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com