
已知函数f(x)=x3+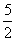 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+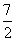 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数).
(I)若g(x)在x=l处的切线方程为y=kx-5(k为常数),求b的值;
(II)设函数f(x)的导函数为f’(x),若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
(III)令F(x)=f(x)-g(x),若函数F(x)存在极值,且所有极值之和大于5+1n2,求a的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
如图,椭圆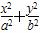 =1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直
=1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直 线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为
线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为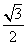 ,且过点A(0,1).
,且过点A(0,1).
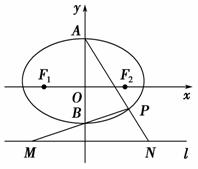
(1)求k1·k2的值;
(2)求MN的最小值;
(3)随着点P的变化,以MN为直径的圆是否恒过定点?若过定点,求出该定点;如不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,a、b、c分别为角A、B、C所对的边,且
(2b+c)cosA+acosC =0
(I)求角A的大小:
(II)求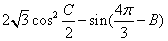 的最大值,并求取得最大值时角 B.C的大小.
的最大值,并求取得最大值时角 B.C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
某学生在高三学年最近九次考试中的数学成绩加下表:

设回归直线方程y= bx+a,则点(a,b)在直线x+5y-10=0的( )
A.左上方 B.左下方 C.右上方 D.右下方
查看答案和解析>>
科目:高中数学 来源: 题型:
直线x=t、y=x将圆x2+y2 =4分成若干块,现用5种不同的颜色给这若干块涂色,且共边的颜色不同,每块只涂一色,共有260种涂法,则实数t的取值范围是____
查看答案和解析>>
科目:高中数学 来源: 题型:
假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天的回报比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报是前一天的两倍.
若投资的时间为 天,为使投资的回报最多,你会选择哪种方案投资?
天,为使投资的回报最多,你会选择哪种方案投资?
(A)方案一 (B)方案二 (C)方案三 (D)都可以
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com