
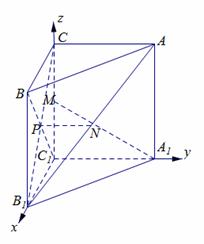
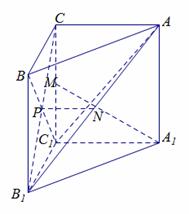
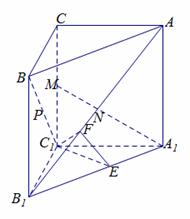
如图4,已知三棱柱ABC—A1B1C1的侧棱与底面垂直,且∠ACB=90°,
∠BAC=30°,BC=1,AA1= ,点P、M、N分别为BC1、CC1、AB1
,点P、M、N分别为BC1、CC1、AB1
的中点.
(1)求证:PN//平面ABC;
(2)求证:AB1⊥A1M;
(3)求二面角C1—A B1—A1的余弦值.

(1)证明:连结CB1,∵P是BC1的中点 ,∴CB1过点P,--1分
∵N为AB1的中点,∴PN//AC,
又∵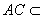 面
面 ,
,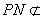 面
面 ,
,
∴PN//平面ABC.
(2)证法一:在直角ΔABC中,∵BC=1,∠BAC=30°,
∴ AC=A1C1=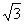
∵棱柱ABC—A1B1C1的侧棱与底面垂直,且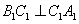 ,以点C1为
,以点C1为
原点,以C1B1所在的直线为x轴建立如图所示空间直角坐标系如图示,则
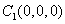 ,
,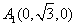 ,
,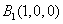 ,
, 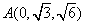 ,
, 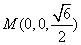
∴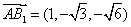 ,
,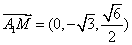
∵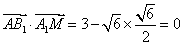
∴ A1M⊥AB1-
【证法二:连结AC1,在直角ΔABC中,∵BC=1,∠BAC=30°,
 ∴ AC=A1C1=
∴ AC=A1C1=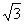
∵
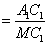 =
=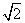 ,
,
∴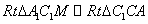 -
-
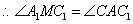 ,
,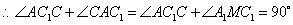
即AC1⊥A1M.
∵B1C1⊥C1A1,CC1⊥B1C1,且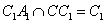
∴B1C1⊥平面AA1CC1,∴B1C1⊥A1M,又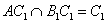 ,故A1M⊥A B1C1,
,故A1M⊥A B1C1,
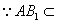 面A B1C1, ∴ A1M⊥AB1.
面A B1C1, ∴ A1M⊥AB1.
【证法三:连结AC1,在直角ΔABC中,∵BC=1,∠BAC=30°,
∴ AC=A1C1=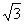 -
-
设∠AC1A1=α,∠MA1C1=β
∵
∴α+β=90° 即AC1⊥A1M.
∵B1C1⊥C1A1,CC1⊥B1C1,且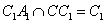
∴B1C1⊥平面AA1CC1,∴B1C1⊥A1M,又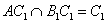
故A1M⊥面A B1C1,
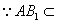 面A B1C1, ∴ A1M⊥AB1.
面A B1C1, ∴ A1M⊥AB1.
(3)解法一:∵棱柱ABC—A1B1C1的侧棱与底面垂直,且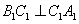 ,
,
 以点C1为原点,以C1B1所在的直线为x轴建立如图所示空间直角坐标系,
以点C1为原点,以C1B1所在的直线为x轴建立如图所示空间直角坐标系,
依题意得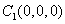 ,
,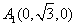 ,
,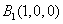 ,
,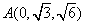 ,
,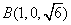 ,
,
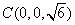 ,
,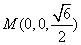
设面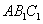 的一个法向量为
的一个法向量为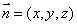
由 得
得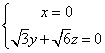 ,令
,令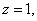 得
得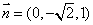 .
.
同理可得面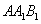 的一个法向量为
的一个法向量为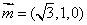 分
分
故二面角的平面角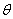 的余弦值为
的余弦值为
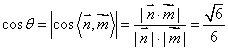 -【解法二:过C1作C1E⊥A1B1交A1B1于点E,过E作EF⊥AB1交AB1于F,连结C1 F,
-【解法二:过C1作C1E⊥A1B1交A1B1于点E,过E作EF⊥AB1交AB1于F,连结C1 F,
 ∵平面AA1BB1⊥底面A1B1C1,∴ C1E⊥平面AA1BB1,
∵平面AA1BB1⊥底面A1B1C1,∴ C1E⊥平面AA1BB1,
∴ C1E⊥AB1,∴ AB1⊥平面C1EF,∴ AB1⊥C1F,
故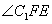 为二面角C1—A B1—A1的平面角,
为二面角C1—A B1—A1的平面角,
在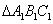 中,
中,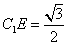 ,
,
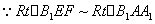 ,
,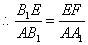 ,-
,-
又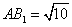 故
故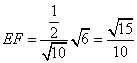
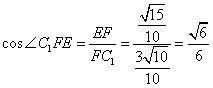


科目:高中数学 来源: 题型:
如图,椭圆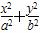 =1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直
=1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直 线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为
线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为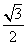 ,且过点A(0,1).
,且过点A(0,1).
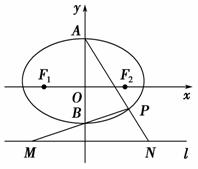
(1)求k1·k2的值;
(2)求MN的最小值;
(3)随着点P的变化,以MN为直径的圆是否恒过定点?若过定点,求出该定点;如不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
直线x=t、y=x将圆x2+y2 =4分成若干块,现用5种不同的颜色给这若干块涂色,且共边的颜色不同,每块只涂一色,共有260种涂法,则实数t的取值范围是____
查看答案和解析>>
科目:高中数学 来源: 题型:
假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天的回报比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报是前一天的两倍.
若投资的时间为 天,为使投资的回报最多,你会选择哪种方案投资?
天,为使投资的回报最多,你会选择哪种方案投资?
(A)方案一 (B)方案二 (C)方案三 (D)都可以
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com