
| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
分析 根据圆的方程求得圆心坐标和半径,进而根据点到直线的距离求得圆心到直线的距离,进而分别求得较短的弧长和较长的弧长的圆心角的关系,答案可得.
解答 解:圆(x-1)2+y2=1的圆心为(1,0)到直线x-y=0的距离为$\frac{1}{\sqrt{1+3}}$=$\frac{1}{2}$,圆的半径为:1,
∴弦长为2×$\sqrt{{1}^{2}-({\frac{1}{2})}^{2}}$=$\sqrt{3}$.小扇形的圆心角为:120°,
∴较短弧长与较长弧长之比为1:2.
故选:A.
点评 本题主要考查了直线与圆相交的性质.在弦与半径构成的三角形中,通过解三角形求得问题的答案.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,4,5} | B. | {4,5} | C. | {-1,1} | D. | {-1,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,1] | B. | (0,1] | C. | [-3,2] | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [157,162) | [162,167) | [167,172) | [172,177) | [177,182) | [182,187) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
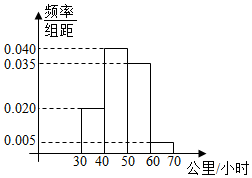 某公路的一个下穿隧道限速60公里/小时,现监控了200辆经过该隧道的车速,将这200个数据作成了频率分布直方图(如图).
某公路的一个下穿隧道限速60公里/小时,现监控了200辆经过该隧道的车速,将这200个数据作成了频率分布直方图(如图).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com