
【题目】对于平面上任意![]() 个点构成的点集
个点构成的点集![]() ,如果其中任意两点之间的距离均已确定,那么就称这个点集是“稳定的”.求证:在
,如果其中任意两点之间的距离均已确定,那么就称这个点集是“稳定的”.求证:在![]() 格点的平面点集
格点的平面点集![]() 中,无三点共线,且其中的
中,无三点共线,且其中的![]() 个两点之间的距离已被确定,那么点集
个两点之间的距离已被确定,那么点集![]() 就是“稳定的”.
就是“稳定的”.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】对于三次函数![]() ,定义
,定义![]() 是
是![]() 的导函数
的导函数![]() 的导函数,经过讨论发现命题:“一定存在实数
的导函数,经过讨论发现命题:“一定存在实数![]() ,使得
,使得![]() 成立”为真,请你根据这一结论判断下列命题:
成立”为真,请你根据这一结论判断下列命题:
①一定存在实数![]() ,使得
,使得![]() 成立;②一定存在实数
成立;②一定存在实数![]() ,使得
,使得![]() 成立;③若
成立;③若![]() ,则
,则![]() ;④若存在实数
;④若存在实数![]() ,且
,且![]() 满足:
满足:![]() ,则函数
,则函数![]() 在
在![]() 上一定单调递增,所有正确的序号是( )
上一定单调递增,所有正确的序号是( )
A. ①② B. ①③ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北![]() 的方向上,仰角为
的方向上,仰角为![]() ,行驶4km后到达B处,测得此山顶在西偏北
,行驶4km后到达B处,测得此山顶在西偏北![]() 的方向上.
的方向上.
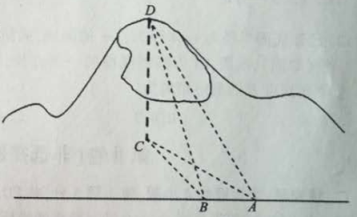
(1)求此山的高度(单位:km);
(2)设汽车行驶过程中仰望山顶D的最大仰角为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一商场对5年来春节期间服装类商品的优惠金额![]() (单位:万元)与销售额
(单位:万元)与销售额![]() (单位:万元)之间的关系进行分析研究并做了记录,得到如下表格.
(单位:万元)之间的关系进行分析研究并做了记录,得到如下表格.
日期 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图,并判断服装类商品的优惠金额与销售额是正相关还是负相关;

(2)根据表中提供的数据,求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(3)若2019年春节期间商场预定的服装类商品的优惠金额为10万元,估计该商场服装类商品的销售额.
参考公式:
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面是水稻产量与施化肥量的一组观测数据(单位:千克/亩):
施化肥量 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
水稻产量 | 320 | 330 | 360 | 410 | 460 | 470 | 480 |
(1)将上述数据制成散点图;
(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直随施化肥量的增加而增长吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活.一媒体为调查市民对低头族的认识,从某社区的500名市民中随机抽取n名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
组数 | 分组(单位:岁) | 频数 | 频率 |
1 |
| 5 | 0.05 |
2 |
| 20 | 0.20 |
3 |
| a | 0.35 |
4 |
| 30 | b |
5 |
| 10 | 0.10 |
合计 | n | 1.00 | |
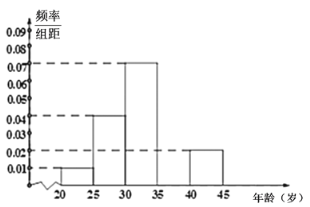
(1)求出表中a,b,n的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定在第2,4,5组中用分层抽样的方法抽取6名市民进行问卷调查,再从这6名1民中随机抽取2名接受电视采访,求第2组至少有一名接受电视采访的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校医务室欲研究昼夜温差大小与高三患感冒人数多少之间的关系,他们统计了2019年9月至2020年1月每月8号的昼夜温差情况与高三因患感冒而就诊的人数,得到如下资料:
日期 | 2019年9月8日 | 2019年10月8日 | 2019年11月8日 | 2019年12月8日 | 2020年1月8日 |
昼夜温差 | 5 | 8 | 12 | 13 | 16 |
就诊人数 | 10 | 16 | 26 | 30 | 35 |
该医务室确定的研究方案是先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再用被选取的2组数据进行检验.假设选取的是2019年9月8日与2020年1月8日的2组数据.
(1)求就诊人数![]() 关于昼夜温差
关于昼夜温差![]() 的线性回归方程
的线性回归方程![]() (结果精确到0.01)
(结果精确到0.01)
(2)若由(1)中所求的线性回归方程得到的估计数据与所选出的检验数据的误差均不超过3人,则认为得到的线性回归方程是理想的,试问该医务室所得线性回归方程是否理想?
参考公式: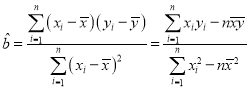 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.
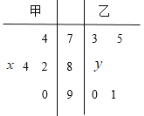
(1)求出x,y的值,且分别求甲、乙两个班中5名学生成绩的方差![]() 、
、![]() ,并根据结
,并根据结
果,你认为应该选派哪一个班的学生参加决赛?
(2)从成绩在85分及以上的学生中随机抽取2名.求至少有1名来自甲班的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com