【题目】某中学高二年级的甲、乙两个班中，需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛，已知这次预赛他们取得的成绩的茎叶图如图所示，其中甲班5名学生成绩的平均分是83，乙班5名学生成绩的中位数是86．
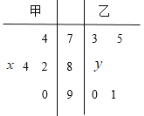
（1）求出x，y的值，且分别求甲、乙两个班中5名学生成绩的方差
、
，并根据结
果，你认为应该选派哪一个班的学生参加决赛？
（2）从成绩在85分及以上的学生中随机抽取2名．求至少有1名来自甲班的概率．
【答案】（1）甲班参加；（2）
．
【解析】
试题（1）由题意知求出x=5，y=6．从而求出乙班学生的平均数为83，分别求出S12和S22，根据甲、乙两班的平均数相等，甲班的方差小，得到应该选派甲班的学生参加决赛．
（2）成绩在85分及以上的学生一共有5名，其中甲班有2名，乙班有3名，由此能求出随机抽取2名，至少有1名来自甲班的概率．
试题解析：（1）甲班的平均分为
，易知
．
；又乙班的平均分为
，∴
；
∵
，
，说明甲班同学成绩更加稳定，故应选甲班参加．
（2）
分及以上甲班有
人，设为
；乙班有
人，设为
，从这
人中抽取人的选法有：
，共
种，其中甲班至少有
名学生的选法有
种，则甲班至少有名学生被抽到的概率为．
科目：高中数学 来源： 题型：
【题目】对于平面上任意
个点构成的点集
，如果其中任意两点之间的距离均已确定，那么就称这个点集是“稳定的”.求证：在
格点的平面点集中，无三点共线，且其中的
个两点之间的距离已被确定，那么点集就是“稳定的”.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，曲线
的参数方程为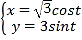
（t为参数）．以坐标原点为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程是
，曲线
的极坐标方程是
．
（1）求直线l和曲线的直角坐标方程，曲线的普通方程；
（2）若直线l与曲线和曲线在第一象限的交点分别为P，Q，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知正方体
（如图），则（ ）
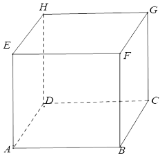
A.直线CF与GD所成的角与向量所成的角
相等
B.向量
是平面ACH的法向量
C.直线CE与平面ACH所成角的正弦值与
的平方和等于1
D.二面角
的余弦值等于
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在“新零售”模式的背景下，某大型零售公司推广线下分店，计划在S市的A区开设分店，为了确定在该区开设分店的个数，该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数，y表示这个x个分店的年收入之和.
(1)该公司已经过初步判断，可用线性回归模型拟合y与x的关系，求y关于x的线性回归方程
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x，y之间的关系为
，请结合(1)中的线性回归方程，估算该公司应在A区开设多少个分店时，才能使A区平均每个分店的年利润最大?
(参考公式:，其中
，
)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题中错误的是（ ）
A. 命题“若
，则
”的逆否命题是真命题
B. 命题“
”的否定是“
”
C. 若
为真命题，则
为真命题
D. 已知
，则“
”是“
”的必要不充分条件
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校为了了解甲、乙两班的数学学习情况，从两班各抽出10名学生进行数学水平测试，成绩如下(单位：分)：
甲班：82 84 85 89 79 80 91 89 79 74
乙班：90 76 86 81 84 87 86 82 85 83
(1)求两个样本的平均数；
(2)求两个样本的方差和标准差；
(3)试分析比较两个班的学习情况．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
