Question

13．已知某几何体的三视图和直观图如图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．

（Ⅰ）求证：B₁N⊥CN；
（Ⅱ）设M为AB中点，在棱BC上是否存在一点P，使MP∥平面B₁CN？若存在，求$\frac{BP}{PC}$的值；若不存在，请说明理由．

Answer 1

分析 （Ⅰ）由三视图可知AN=4，BB₁=8．在直角梯形ANB₁B中，取BB₁的中点H，连结NH，证明B₁N⊥平面BCN，即可证明：B₁N⊥CN；
（Ⅱ）在直角梯形ANB₁B中，取BH中点Q，由题意得四边形ANB₁H是平行四边形，利用面面平行，确定线面平行即可得出结论．

解答 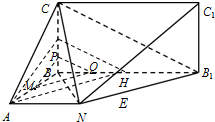（Ⅰ）证明：由三视图可知AN=4，BB₁=8．
在直角梯形ANB₁B中，取BB₁的中点H，连结NH．
可得NH⊥BB₁，则ABHN是正方形．
所以BN=4$\sqrt{2}$，NH=BH=HB₁=4，NB₁=4$\sqrt{2}$．
可得$B{N}^{2}+N{{B}_{1}}^{2}$=$B{{B}_{1}}^{2}$，所以BN⊥NB₁．
因为BN∩BC=B，所以B₁N⊥平面BCN，则B₁N⊥CN．
（Ⅱ）解：在直角梯形ANB₁B中，取BH中点Q，由题意得四边形ANB₁H是平行四边形．
所以AH∥B₁N∥MQ．
因为NB₁?平面CNB₁，MQ?平面CNB₁，所以MQ∥平面CNB₁．
又因为MP∥平面CNB₁，MP∩MQ=M，所以平面MPQ∥平面CNB₁．
且平面MPQ∩平面BCC₁B₁=PQ，平面CNB₁∩平面BCC₁B₁=CB₁，所以PQ∥CB₁．
所以$\frac{BP}{PC}$=$\frac{BQ}{Q{B}_{1}}$=$\frac{1}{3}$．

点评 本题主要考查三视图，直线与平面的平行的判定和性质，直线与平面的垂直的判定和性质，属于中档题．